Olá, estudante, bem-vindo (a). Vamos fazer uma revisão dos conceitos principais e básicos para seguirmos em frente em nosso estudo sobre mecânica. Boa aula!
A mecânica é um ramo da física que se destina ao estudo dos efeitos das forças sobre os objetos. Entre os vários tópicos de física, este é o que tem maior interesse para os engenheiros, devido ao seu vasto campo de aplicabilidade nos campos de vibrações, equilíbrio dos corpos, estabilidade e resistência de máquinas, desempenho de motores, escoamento de fluidos, estruturas dos sólidos, comportamento molecular, atômico e subatômico, entre vários outros.
Um entendimento completo dessa disciplina é pré-requisito fundamental para trabalhar nessas áreas e principalmente nos campos da engenharia civil. É inadmissível que um engenheiro civil desconheça os princípios básicos que regem a mecânica.
Em uma abordagem mais histórica, a mecânica é uma ciência antiga. Pode-se até dizer que é uma das mais antigas das ciências físicas. Os primeiros relatos escritos datam de 200 a.C., sobre o princípio da alavanca e o princípio da flutuação, ambos de Arquimedes. Mais tarde, em meados do sec. XVI, Galileu elaborou uma investigação sobre quedas de pedras, nascia, assim, a dinâmica. A consolidação da mecânica em forma de leis foi atribuída a Newton, juntamente com sua lei universal da gravitação, já no sec. XVII. Newton também contribuiu para o cálculo infinitesimal na análise matemática. Aprimoramentos e contribuições foram formulados por da Vinci, Varignon, Euler, D’Alembert, Lagrange, Laplace, entre outros renomados.
Vamos, então, nos aventurar no universo dos princípios da mecânica e de suas aplicações!
Veremos que o rigor matemático estará entrelaçado aos conceitos físicos desta disciplina, tendo papel importante na resolução dos problemas. O conteúdo de mecânica é subdivido em duas partes: a estática e a dinâmica. A estática trabalha com os corpos em equilíbrio e suas causas, enquanto a dinâmica se fundamenta na investigação do movimento dos corpos e de suas acelerações. Faremos, a seguir, uma breve recapitulação dos conceitos mais relevantes que vamos constantemente trabalhar ao longo deste curso.
Aqui, vamos recapitular alguns conceitos e definições fundamentais que você deverá ter em mente para que possa ter um bom desempenho durante o curso.
Esses conceitos devem ser entendidos desde o início para que não haja confusão ao longo da exposição do conteúdo relativo à mecânica.
O espaço é a região geométrica que é ocupada pelos corpos e cuja posição é fornecida por medidas lineares e angulares, desde que definido um sistema de coordenadas. Em mecânica, vamos trabalhar bastante com problemas planos (bidimensionais) e espaciais (tridimensionais) e a escolha de um sistema de coordenadas que respeite a simetria do problema é primordial. Assim, de acordo com as características dos problemas, poderão ser utilizadas as coordenadas usuais cartesianas, polares, cilíndricas e esféricas.

O tempo é uma grandeza física destinada à medida de sucessão de eventos. Essa grandeza é puramente dinâmica e não será utilizada nos problemas de estática. Para obter um olhar mais filosófico sobre o tempo, leia no hypescience.com, uma materia vocês podem acessar o link a seguir.
O que é o tempo?
A massa é uma propriedade inerente aos corpos que é a medida da inércia de deste. Do ponto de vista químico, a massa nada mais é do que a quantidade de matéria em um corpo.
A força é definida pela ação de um corpo sobre o outro. Quando dois ou mais corpos interagem, dizemos que existe uma força entre eles. Uma força é capaz de acelerar um corpo na direção de sua aplicação.
Uma partícula ou um ponto material é um corpo cujas suas dimensões podem ser desprezadas em relação a outros corpos envolvidos nos problemas. Por exemplo, um veículo que trafega na BR 060 tem suas dimensões de comprimento e largura desprezadas em relação à extensão da rodovia e podemos considerá-lo como apenas um ponto se deslocando no espaço.
Um corpo pode ser considerado um corpo rígido quando duas partículas que constituem esse corpo mantêm sua distância fixa “rígida”, ou seja, a variação da distância entre quaisquer duas partículas de um corpo é nula ou desprezível. A título de exemplo, considere a figura a seguir.

A figura localiza dois pontos, A e B, de um mesmo corpo num sistema de coordenadas cartesiano tridimensional Oxyz. Os vetores r\(_{A}\) e r\(_{B}\) localizam respectivamente as partículas A e B do corpo rígido, enquanto o vetor r\(_{AB}\) representa a distância relativa de B em relação a A. O corpo da Figura 1 somente será considerado um corpo rígido se, e somente se:
Ou seja, se a taxa de variação d
\[\frac{{dr}_{AB}}{dt}=0 ~~~~~~~ (0.1)\]
o vetor posição relativa de quaisquer duas partículas constituintes de um corpo rígido forem nulas, a equação 1.1 pode ser chamada de condição de corpo rígido.

As três leis de Newton são conhecidas como princípios basilares da mecânica clássica, também conhecida como mecânica newtoniana. Para conhecer um pouco mais sobre o Sir. Isaac Newton, eu recomento o link a seguir.
Isaac Newton: Fé e Física.
Essas leis permitem descrever e governar o movimento. Desse modo, apresentaremos a seguir as três leis com enunciados modernos para facilitar o entendimento.

A Primeira Lei de Newton, ou princípio da inércia, diz que um corpo tende a manter seu estado de equilíbrio a menos que aja sobre ele a ação de uma força resultante.
Esse enunciado traz dois conceitos bastante importantes. O primeiro é o de estado de equilíbrio. O equilíbrio pode ser estático ou dinâmico. No equilíbrio estático, a partícula está em repouso, ou seja, sua velocidade é nula, enquanto no equilíbrio dinâmico a partícula se encontra em movimento retilíneo uniforme (MRU). O segundo conceito importante é o de força resultante. A força resultante é o somatório vetorial de todas as forças que atuam num corpo. Para ilustrar esse conceito, veja a Figura 2.

O corpo da Figura 2 está sob a ação de n forças. Esse sistema pode ser substituído por um sistema mais simples que contenha apenas uma força, a força resultante, que possui o mesmo efeito das n forças. Matematicamente, podemos expressar a força resultante da seguinte forma:
\[ {\overrightarrow{F}}_{1} + {\overrightarrow{F}}_{2} + {\overrightarrow{F}}_{3}+ \cdots +{\overrightarrow{F}}_{n} = \sum_{i=1}^{n} {F}_{i}= {F}_{R}~~~~~~~(0.2) \]
Onde o somatório é realizado sobre todas as forças que atuam na partícula e \({\overrightarrow{F}}_{R}\) representa a força resultante.

A Segunda Lei de Newton, ou princípio fundamental da dinâmica, diz que a força resultante é diretamente proporcional à aceleração e aponta na mesma direção dela.
Em termos matemáticos, a segunda lei de Newton pode ser escrita da seguinte maneira:
\[F_r=ma~~~~~~~ (0.3)\]

A Terceira Lei de Newton, ou princípio da ação e reação, diz que toda ação corresponde a uma reação de mesma intensidade, mesma direção, mas de sentido oposto.
Para entender esse princípio, considere que duas partículas A e B interajam pela a ação de uma força de campo como representado na Figura 3.
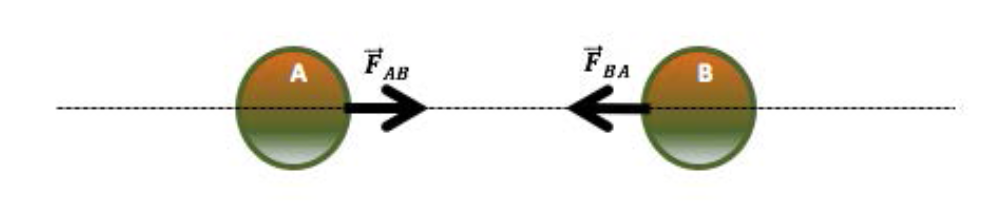
Neste caso, se o corpo A sofre a ação de uma força devido à presença do corpo B, o corpo B sofrerá a ação de uma força devido à presença do corpo A de mesma intensidade mesma direção, mas com sentido oposto. Com efeito:
\[\overrightarrow{F}_{ab}= - \overrightarrow{F}_{ba} ~~~~~~~(0.4)\]
As quatro grandezas fundamentais da mecânica são o comprimento, a massa, o tempo e a força. As unidades de escolha dessas grandezas devem ser consistentes com as equações de Newton enunciadas acima e, portanto, não podem ser escolhidas arbitrariamente. O Sistema Internacional de Unidades, abreviado por SI (Système Internacional d’Unités) será utilizado durante todo o curso. A tabela a seguir correlaciona as grandezas básicas da mecânica com suas respectivas unidades de medida no SI e os símbolos utilizados para representá-las.

Como apresentado na tabela, as unidades de massa (kg), de comprimento (m) e de tempo (s) são unidades básicas (ou fundamentais), enquanto a unidade de força (N) é derivada das anteriores a partir da equação 1.3. Desse modo, temos:
\[N=kg.m/s^{2}\]
Portanto, 1 newton é a quantidade de força necessária para acelerar uma massa de 1 kg a 1 m/s².
Em mecânica, precisamos frequentemente determinar o peso de um corpo, que nada mais é do que a força gravitacional que atua sobre ele. Newton também foi responsável por equacionar a lei de atração gravitacional entre os corpos. Assim, temos:
\[F=G\frac{m_1 m_2}{r^2}~~~~~~~ (0.5)\]
Onde F é a força de atração mútua entre as partículas, G é a constante universal da gravitação, m\(_{1}\) e m\(_{2}\) são as massas das duas partículas envolvidas e r é a distância que separa seus centros.
Nas proximidades da superfície terrestre, a força gravitacional entre os corpos e a terra passa a ser chamada de força peso e usamos a letra W para indicar essa força. Além disso, os corpos ficarão sujeitos à aceleração da gravidade g = 9.81 m/s².
Uma das grandes dificuldades que os alunos encontram para resolver os problemas de mecânica é entender o que está sendo pedido nos enunciados das questões. Basicamente, uma questão de interpretação de texto. Dessa maneira, eu recomendo fortemente que os alunos sublinhem o que está sendo pedido no enunciado dos problemas e, além disso, anotem os valores das variáveis fornecidas nos problemas. Isto os ajudará a correlacionarem as variáveis fornecidas com as variáveis faltantes. Está tática ajuda bastante no entendimento dos problemas de mecânica.
Elaborado o digrama do corpo livre, a escolha correta do sistema de coordenadas facilita na resolução de alguns problemas. A simetria dos problemas, quando houver, ajuda na escolha do sistema de referência. Assim, a título de exemplo, um problema que pode ser bastante complicado para ser solucionado em coordenadas retangulares, poderá ser simplificado a partir da aplicação de um sistema de coordenadas polares.
Realizados os passos anteriores, é importante que o aluno estabeleça uma estratégia para aplicação dos princípios básicos da mecânica. Esses princípios e táticas serão abordadas ao longo do curso e é de extrema importância um bom entendimento desses conceitos antes de partir para os exercícios. Assim, a junção teoria/prática só é alcançada quando se tem a teoria bem fundamentada.
Jamais se esqueçam de checar as unidades de medidas das grandezas físicas envolvidas. Vários alunos erram na solução dos problemas, pois deixaram de converter as unidades de medidas das variáveis físicas para as unidades do SI. Fiquem bastante atentos em relação a isso.
Por fim, sempre verifiquem sua resposta final. Ao chegarem no resultado, chequem se o valor encontrado está em concordância com outras variáveis envolvidas nos problemas ou com seus conhecimentos prévios sobre o assunto. Para isso, é importante verificar ordem de grandeza, unidade de medida, sinal de menos, entre outros fatores.
Em mecânica, vamos trabalhar com dois tipos de grandezas: as escalares \(^{4}\) e as vetoriais.

As grandezas escalares são caracterizadas por apenas um valor e sua unidade de medida, por exemplo, o tempo, o volume, a energia e a massa. Já as grandezas vetoriais possuem direção e sentido, além de seu valor e unidade de medida.
Podemos citar como exemplo de grandezas vetoriais a força, a velocidade e a aceleração. Podemos representar um vetor através da seguinte notação\(\overrightarrow{A}\), que indica “vetor A”. Além disso, podemos indicar um vetor utilizando a notação em negrito A, que também indica “vetor A”. Aqui, vamos utilizar as duas notações para que o aluno se familiarize com as diversas formas de representação vetorial. A figura a seguir mostra uma representação dos elementos que compõem um vetor: a cauda, a ponta e a linha de ação.

Vamos agora abordar algumas operações com vetores que serão corriqueiras durante seus estudos
Seja um vetor A e um escalar 𝛼. O produto do vetor pelo escalar A pelo escalar 𝛼 é definido por um vetor de intensidade |𝛼𝐴|. A direção do vetor resultante é a mesma do vetor A e o sentido depende do sinal do escalar 𝛼. Se 𝛼 for um número positivo, então, o sentido do vetor resultante |𝛼𝐴| é o mesmo do vetor A. Em contrapartida, se 𝛼 for um número negativo, o sentido do vetor resultante será o oposto do vetor A. O valor negativo de um vetor (ou seu vetor oposto) é obtido multiplicando-o por (-1), como indicado na figura a seguir.

A divisão de um vetor é definida utilizando as regras de multiplicação por um escalar, uma vez que, \(A/a = (1/a) A\) com \(a\neq0\). Escolhemos algumas operações para serem representadas na figura seguinte.

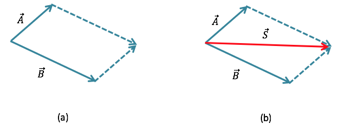
A soma vetorial será realizada dois a dois. Considere dois vetores A e B representados na Figura 7.

Eles podem ser somados de modo a gerar um vetor soma resultante S. Utilizamos a regra do paralelogramo para operacionar somas vetoriais. Primeiramente, unimos as caudas dos dois vetores e, em seguida, duplicamos os vetores nas extremidades opostas, como indicado na figura 8(a). O vetor soma resultante é obtido unindo as caudas dos vetores com as pontas como mostra a figura 8(b).
Um caso particular ocorre quando dois vetores são colineares, ou seja, ambos estão sobre a mesma linha de ação. Nesse caso, não aplicamos a regra do paralelogramo e a soma é realizada algebricamente (Figura 9).

A diferença D entre dois vetores A e B pode ser representada da seguinte maneira:
\[\overrightarrow{D}=\overrightarrow{A} -\overrightarrow{B} =\overrightarrow{A}+ (-\overrightarrow{B})\]
Vamos considerar os mesmos dois vetores A e B da Figura 7. Para determinarmos o vetor diferença, devemos, primeiro, obter o vetor oposto de B. Feito isso, o procedimento para obtenção do vetor diferença é semelhante à soma vetorial representada na Figura 8. Ilustramos esse procedimento na figura a seguir.

Um vetor pode ser decomposto em duas ou mais componentes dependendo do sistema de referência adotado. Por exemplo, a Figura 11 mostra um vetor V qualquer decomposto ao longo de duas retas a e b.

As operações vetoriais tridimensionais são simplificadas, uma vez que aplicamos a forma vetorial cartesiana, ou seja, utilizamos o sistema de referência retangular. Esse sistema obedece à regra da mão direita, o polegar aponta para o eixo z enquanto os dedos abertos apontam na direção x e, quando fechados, apontam na direção y como representado na figura a seguir.

Um vetor A é representado nesse sistema pelas componentes A\(_{x}\), A\(_{y}\) e A\(_{z}\), enquanto a projeção do vetor A no plano xy é representada pelo vetor A’, como mostra a Figura 13.

A direção do vetor A pode ser indicada pelo vetor unitário que possui esse nome devido à sua intensidade ser igual a 1. Matematicamente, representamos um vetor unitário da seguinte maneira:
\[{u}_{a}=\frac{\overrightarrow{A}}{ | \overrightarrow{A} |}~~~~~~~ (0.6)\]
Nesse sentido, podemos representar o sistema de coordenadas cartesianas pelos vetores unitários cartesianos \(\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}\), que apontam para as direções cartesianas x, y e z, respectivamente, de modo que um vetor A, quando representado nesse sistema, pode ser escrito como:
\[\overrightarrow{A}=A_{x}\widehat{i} + A_{y}\widehat{i}+A_{z}\widehat{i}~~~~~~~(0.7) \]
A principal vantagem de escrevermos um vetor como escrito na equação 2.2 é que decompomos o vetor nas direções cartesianas e, a partir disso, podemos realizar operações vetoriais componente a componente algebricamente. Assim, a intensidade do vetor A pode ser obtida por:
\[\overrightarrow {A=}\sqrt{A^2_{x}+ A^2_{y}+A^2_{z}}~~~~~~~ (0.8)\]
Sejam dois vetores A e B representados por:
\[\begin{cases}\overrightarrow{A} = A_{x}\widehat{i}+A_{y}\widehat{j}+A_{z}\widehat{k}\\\overrightarrow{B}=B_{x}\widehat{i}+B_{y}\widehat{j}+B_{z}\widehat{k} \end{cases} \]
A soma vetorial pode ser obtida por:
\[\overrightarrow{S}=\overrightarrow{A}+\overrightarrow{B}=({A_{x}}+{b_{x}})\widehat{i}+({A_{y}}+{b_{y}})\widehat{j}+({A_{z}}+{b_{z}})\widehat{k}(0.9)\]
Enquanto a diferença é representada por:
\[\overrightarrow{D}=\overrightarrow{A}-\overrightarrow{B}=(A_{x}-b_{x})\widehat{i}+(A_{y}-b_{y})\widehat{j}+(A_{b}-A_{z})\widehat{k}(0.10)\]
No caso de um sistema de forças concorrentes, ou seja, várias forças atuando sobre um mesmo objeto, podemos representar a força resultante pela seguinte equação:
\[{F}_r=\sum{F}=\sum{F}_x\widehat{i}+\sum{F}_y\widehat{j}+\sum{F}_z\widehat{k}(0.11)\]
Onde\(\scriptstyle\sum{F}_x+\sum{F}_y+\sum{F}_z \)representam as somas algébricas das componentes x, y, z de cada força que atua no sistema.
O produto escalar é por várias vezes utilizado em mecânica para calcular o ângulo em dois vetores. Considere dois vetores A e B como representados na Figura 14.

O produto escalar (ou produto interno) dos vetores A e B é escrito como \(\overrightarrow{A}\cdot\overrightarrow{B}\), lido como “A escalar B” e expresso matematicamente por:
\[\overrightarrow{A}\cdot\overrightarrow{B}=AB \cos \theta ~~~~~~ (0.12)\]
No plano cartesiano, os vetores unitários \(\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}\) definem uma matriz de produto escalar cujos resultados são:
\[\begin{array}[b]{r}{\widehat{i}\cdot\widehat{i}=1 \\ \widehat{j}\cdot\widehat{i}=0 \\ \widehat{k}\cdot\widehat{i}=0} \end{array} ~~~~~~~~~~~~~ \begin{array}[b]{r}{\widehat{i}\cdot\widehat{j}=0 \\ \widehat{j}\cdot\widehat{j}=1 \\ \widehat{k}\cdot\widehat{j}=0} \end{array} ~~~~~~~~~~~~~ \begin{array}[b]{r}{\widehat{i}\cdot\widehat{k}=0 \\ \widehat{j}\cdot\widehat{k}=0 \\ \widehat{k}\cdot\widehat{k}=1} \end{array}~~~~~~~ (0.13)\]
Os estudantes devem saber bem esses resultados, pois os utilizaram rotineiramente durante a disciplina de Mecânica.
Em termos das componentes, utilizando as equações 2.7 e 2.8, podemos escrever o produto interno da seguinte forma:
\[\overrightarrow{A}\cdot\overrightarrow{B}=A_{x}B_{x}+A_{y}B_{y}+A_{z}B_{z} ~~~~~~~(0.14)\]
Aula Concluída!
Avançar