Olá, estudante, bem-vindo(a). Nesta aula, vamos investigar quais são as condições necessárias e suficientes para manter um corpo rígido em equilíbrio. Vimos, nas aulas passadas, quais eram as condições para obter um ponto material em equilíbrio, agora, vamos expandir esses conceitos ao corpo rígido. Boa aula!
Vamos iniciar nossa discussão analisando o corpo rígido da figura a seguir, onde localizamos uma partícula i no seu interior.

Ao analisarmos o diagrama do corpo livre dessa i-ésima partícula, é possível verificar que apenas duas forças atuam sobre ela: f\(_{i}\), que é o somatório das interações entre as partículas que compõem o corpo rígido, ou seja, a resultante de forças internas, e F\(_{i}\), que é a resultante das forças externas. Como exemplo, podemos citar a força peso, forças de contato, interações eletromagnéticas, entre outras. A primeira lei de Newton pressupõe o equilíbrio na seguinte forma:
\[f_i+F_i=0 ~~~~~~~(5.1)\]
Essa é a condição de equilíbrio para apenas uma partícula que compõe o corpo rígido. Para todas as partículas, teremos:
\[f_i+F_i=0~~~~~~~(5.2)\]
Um detalhe muito importante deve ser levado em conta. Se considerarmos as partículas aos pares, veremos que o somatório das forças internas para esse par deve ser nulo, pois se trata de um par ação e reação. Consequentemente, temos que, para um corpo rígido, o somatório das forças internas é zero. Com efeito, temos:
\[\sum F=0~~~~~~~(5.3)\]
Passamos agora à análise dos momentos das forças que atuam sobre a i-ésima partícula em relação a um ponto arbitrário qualquer O, como na Figura 2.

Utilizando a equação \({M}_{O}= r \times F\) para o momento da força e a propriedade distributiva do produto vetorial, podemos obter:
\[r_{1} \times(f_1+F_i)=r_i \times f_i+f_i+r_i\times F_i=0\]
Aplicando para todas as partículas que compõem o corpo rígido, temos:
\[\sum r_1\times f_1+F_1=0\]
O primeiro termo dessa equação se torna nulo uma vez que o somatório das forças internas de um corpo rígido é zero. Portanto, podemos usar a seguinte notação \(\sum M_o= \sum r_1 \times F_1\)para escrevermos:
\[\sum M_o=0~~~~~~~(5.4)\]
Desse modo, podemos resumir as condições de equilíbrio para um corpo rígido da seguinte maneira:
\[\sum F=0\]
\[\sum M_0=0\]
Para aplicarmos corretamente as condições de equilíbrio, temos que especificar as forças que atuam no corpo, e não há maneira melhor do que elaborar um diagrama de corpo livre para fazer isso. É nesse esboço que todas as forças que atuam no corpo são levadas em consideração, assim como seus efeitos.
Vamos considerar, antes disso, alguns tipos de reações que surgem em apoio entre os corpos e um sistema de forças coplanares.

Definimos apoio como sendo algo que impeça a translação de um corpo. Desse modo, uma força é aplicada na direção da tendência de translação. O mesmo ocorre no caso da rotação de um corpo rígido.
Como exemplo, considere a figura a seguir. Nesta figura, está representada uma viga apoiada sobre um rolete ou cilindro. Nesse caso, o apoio impede que a viga sofra uma translação na vertical e, portanto, pode exercer apenas uma força nessa direção.


Exemplos de outros tipos de apoios podem ser encontrados acessando
Mecânica Técnica Aula 16
Um detalhe bastante importante na construção de diagramas de corpo livre é o fato de que forças internas não devem ser representadas, apenas as forças externas são consideradas para sua elaboração.
Vimos nas seções anteriores que as condições de equilíbrio se resumem a \(\sum F=0\)e \(\sum M_0=0\). Entretanto, se o corpo rígido estiver sob a ação de forças no plano cartesiano xy, as forças podem ser decompostas nessas direções. Com efeito, podemos escrever as condições de equilíbrio da seguinte maneira:
\(\sum f_x=0 \\ \sum f_y=0 \\ \sum M_o=0 ~~~~~~~(5.6)\)
Onde as somas representam somas algébricas e não mais somas vetoriais, como antes representadas nas equações 5.5.
Vamos iniciar nossas discussões considerando o corpo rígido da figura a seguir. Esse corpo rígido recebe o nome de elemento de duas forças. Neste caso, observamos que esse corpo não está sujeito a nenhuma rotação, e as forças que atuam sobre ele estão localizadas em dois pontos específicos, que podem ser somadas para obtermos as resultantes em A, F\(_{A}\) e em B, F\(_{B}\).

Observe ainda que essas duas forças mantêm o chamado equilíbrio translacional, ou equilíbrio de forças (\(\sum F=0\)), desde que F\(_{A}\) e F\(_{B}\) sejam iguais em intensidade, direção, mas de sentidos opostos. Já o equilíbrio rotacional ou de momento é satisfeito se as forças forem colineares, como mostra a figura anterior.
Já na situação em que o corpo rígido estiver sujeito à ação de três forças, o equilíbrio será satisfeito se as forças forem concorrentes, como na Figura 5(a), ou paralelas, como na Figura 5(b).


Para se aprofundar mais sobre condições de equilíbrio no plano e reações de apoio eu recomendo acessar o link a seguir.
Princípios físicos básicos para as condições de equilíbrio.
Resolveremos vários problemas em estática de corpos rígidos desenhando um diagrama de corpo livre e, para isso, é necessário ter conhecimento de algumas reações de apoio.
Dessa maneira, você, estudante, deve, além de acessar os links propostos, procurar outras fontes e bibliografias.
É de suma importância que você entenda como as forças e os momentos são desenvolvidos por cada apoio. Considere, por exemplo, uma junta esférica, como na figura a seguir.

Essa junta impede qualquer translação no ponto de conexão. Assim, a força que atua nessa junta tem três componentes, F\(_{x}\), F\(_{y}\) e F\(_{z}\), que, após determinados seus valores, podem ser utilizados para determinação da intensidade da força de reação F, \(F=\sqrt{F_x}+ F_y+ F_z\), e cuja orientação depende dos ângulos diretores. Podemos verificar que as componentes das forças podem rotacionar livremente em torno de qualquer eixo e, portanto, não existe resistência a nenhum momento.
Prosseguiremos com o procedimento padrão para elaborar um diagrama de corpo livre. De início, isolamos o corpo desenhando apenas seu contorno e, em seguida, identificamos com cuidado todas as forças e momentos em relação ao sistema de coordenadas que melhor couber; em geral, o sistema de coordenadas cartesiano.
É de práxis adotar como positivas as componentes de reação que tenham intensidades desconhecidas. Se no futuro obtivermos um valor negativo, o sentido da componente será oposto ao preconizado incialmente.

Alguns exemplos de cálculos de reações podem ser encontrados no link a seguir. Acesse e saiba ainda mais!
Mecânica Técnica.
Como já discutimos anteriormente, para que um corpo rígido submetido à ação de forças tridimensionais se mantenha em equilíbrio, é necessário que a força resultante e o momento resultante sejam nulos e, dessa forma, o equilíbrio pode ser expresso como:
\(\sum F=0~~~~~~~(5.7)\)
Onde \(\sum F \) representa o somatório vetorial das forças externas que atuam sobre o corpo rígido, e \(\sum F
\) é a soma vetorial de todos os momentos de binários e momentos de todas as forças em relação a qualquer ponto.
Como lidamos com casos de sistemas de forças tridimensionais, podemos escrever:
\[\sum F=\sum F_x\widehat{i}+\sum F_y\widehat{j}+\sum F_z\widehat{k}=0 ~~~~~~~(5.8)\]
E essas equações somente são satisfeitas quando:
\(\sum Fx= 0\) \(\sum Fy= 0\) \(\sum Fz= 0 ~~~~~~~(5.9)\)
E:
\(\sum Mx= 0\)
\(\sum My=0\)
\(\sum Mz=0\ ~~~~~~~(5.10)\)
Essa seis equações de equilíbrio são equações escalares e podem ser resolvidas apenas para, no máximo, seis incógnitas mostradas num diagrama de corpo livre.
Existem situações nas quais os corpos rígidos podem ter mais apoios do que o necessário para mantê-lo em equilíbrio. E há, porém, outras situações nas quais os corpos não podem ter os apoios suficientes ou eles foram colocados de uma maneira que eles sofram desmoronamento.
Nas situações em que o corpo tem restrições redundantes, mais apoios do que o necessário para manter-se em equilíbrio, dizemos que seu estado de equilíbrio é estatisticamente indeterminado.
Em outras palavras, há mais incógnitas no corpo do que equações de equilíbrio disponíveis para solução do problema.
Para ilustrarmos essa situação, considere a figura a seguir.

A Figura 8 mostra o diagrama de corpo livre da barra.

Esse é um problema estatisticamente indeterminado. Nesse caso, observamos a presença de cinco incógnitas, M\(_{A}\), A\(_{x}\), A\(_{y}\), B\(_{y}\) e C\(_{y}\), e temos apenas três equações de equilíbrio, que são \(\sum My=0\), \(\sum F=0\)e \(\sum M=0\). Desse modo, não podemos determinar todas as variáveis, uma vez que não temos o número de equações suficientes para solução do problema.
Há também casos de restrições inadequadas em que o número de equações é igual ao número de incógnitas, entretanto, o corpo pode ficar instável devido a restrições realizadas de forma inadequada.
Os alunos podem encontrar exemplos e ilustrações dessas restrições nos links citados anteriormente.
Existem casos nos quais um corpo pode ter menos forças de reação do que equações de equilíbrio que podem ser satisfeitas e são chamados de parcialmente restritos. Vamos considerar o caso da figura seguinte juntamente com seu diagrama de corpo livre.
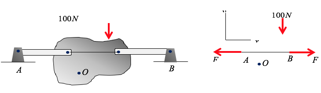
Observe que o ponto O não está localizado sobre a linha AB e, portanto, a equação \(\sum Fx= 0\) nos fornece \(F_a=F_b\) e momento resultante nulo. Porém, \(\sum Fx= 0\)não pode ser satisfeita pela presença da força de 100N e, portanto, o equilíbrio não será obedecido.
Quando um número mínimo de forças reativas for necessário para restringir adequadamente o corpo rígido, o problema será estatisticamente determinado e as equações de equilíbrio podem ser, então, utilizadas para a correta determinação de todas as forças de reação.
Assim, alguns pontos importantes que resumem esta aula podem ser arrolados a seguir:
Para evitarmos a instabilidade de um corpo, exige-se que as linhas de ação das reações não interceptem um eixo comum e não sejam paralelas entre si.
Aula Concluída!
Avançar