Nesta aula, faremos uma abordagem sobre a cinemática que visa investigar o movimento propriamente dito sem se preocupar com as causas deste e nas aulas subsequentes as causas do movimento será estudo a partir de três metodologias distintas.
Para estudarmos a teoria por trás do movimento, precisamos, antes de tudo, definir algumas quantidades físicas. Inicialmente, vamos tratar do movimento retilíneo, ou seja, num certo instante t, o móvel vai ocupar uma posição sobre uma linha reta. Para definirmos a posição P de um móvel, vamos escolher uma origem O fixa na linha reta e um sentido positivo, ambos escolhidos de maneira completamente arbitrária, como indicado na figura a seguir. No Sistema Internacional de Medidas (SI), a posição é dada em metros (m).

Uma vez definida a posição do móvel, podemos falar de velocidade mídia, definida pelo quociente da variação de espaço \(\Delta x\) pelo intervalo de tempo \(\Delta t\):
\[{v_m} = \frac{{\Delta x}}{{\Delta t}} ^{ (13.1)}\]
A velocidade instantânea de um móvel é obtida a partir da definição de velocidade mídia e dada por:
\[v = \mathop {\lim }\limits_{\Delta t \to 0} \frac{{\Delta x}}{{\Delta t}} = \frac{{dx}}{{dt}} ^{ (13.2)}\]
O que é justamente a definição da derivada do espaço em relação ao tempo, ou seja, a taxa de variação do espaço com relação ao tempo. No S.I., a unidade de medida de velocidade é o metro por segundo (m/s).
Nesse mesmo contexto, podemos definir a aceleração mídia:
\[{a_m} = \frac{{\Delta v}}{{\Delta t}} ^{ (13.3)}\]
E também a aceleração instantânea:
\[a = \mathop {\lim }\limits_{\Delta t \to 0} \frac{{\Delta v}}{{\Delta t}} = \frac{{dv}}{{dt}} ^{ (13.4)}\]
Esta última define a taxa de variação da velocidade em relação ao tempo. No S.I., a aceleração é dada em \(m/s^{2}\). Observe que é possível escrever a aceleração instantânea da seguinte maneira:
\[a = \frac{{dv}}{{dt}} = \frac{d}{{dt}}\left( {\frac{{dx}}{{dt}}} \right) \Rightarrow a = \frac{{{d^2}x}}{{d{t^2}}} ^{ (13.5)}\]
Essa é a segunda derivada da posição em relação ao tempo. Além disso, utilizando a regra da cadeia, podemos escrever:
\[a = \frac{{dv}}{{dt}} = \frac{{dv}}{{\color {red} {dx}}}\frac{{\color {red}{dx}}}{{dt}}\]
E, identificando \(v = \frac{{dx}}{{dt}}\), temos:
\[a = v\frac{{dv}}{{dx}} ^{ (13.6)}\]
A equação 13.6 será útil para obtermos outras equações de cinemática que serão úteis ao longo do curso, como veremos nas seções seguintes.
Este é o tipo de movimento que é frequentemente aproximado por várias situações cotidianas de engenharia, em que a aceleração do móvel é nula para todo valor de t. O que implica diretamente em:
\[\frac{{dx}}{{dt}} = v = {\rm{constante}} ^{ (13.7)}\]
Desse modo, a coordenada da posição x, pode ser obtida diretamente a partir de integração da equação 13.7. Rearranjando os termos desta equação, chagamos a:
\[dx = vdt\]
E integrando ambos os lados na respectivas variáveis, temos:
\[\int\limits_{{x_0}}^x {dv} = v\int\limits_0^t {dt} \]
\[x - {x_0} = vt\]
\[\therefore x = {x_0} + vt\]
Esta equação é chamada de equação horária do espaço no movimento retilíneo uniforme e somente poderá ser utilizada se a velocidade do móvel é constante, ou seja, ele percorre espaços iguais em tempos iguais.
Outro exemplo de situação ideal que pode ser aproximada em situações práticas de engenharia é o movimento retilíneo uniformemente variado (MRUV), no qual a aceleração do móvel é constante:
\[\frac{{dv}}{{dt}} = a = {\rm{constante}} ^{ (13.8)}\]
Nesse, a velocidade do móvel é obtida por simples integração da equação 13.8. Assim, rearranjando os termos:
\[dv = adt\]
E integrando em relação às respectivas variáveis, temos:
\[\int\limits_{v0}^v {dv} = a\int\limits_o^t {dt} \]
Note que a aceleração saiu da integração, pois ela é uma constante, da mesma forma como a velocidade também saiu na integração da equação 13.7. Resolvendo a integral, obtemos:
\[v - {v_0} = at\]
\[\therefore v = {v_0} + at ^{ (13.9)}\]
A equação 13.9 é chamada de equação horária da velocidade no movimento retilíneo uniformemente variado. Para determinarmos a posição, podemos substituir a equação 13.7 na equação 13.9:
\[\frac{{dx}}{{dt}} = {v_0} + at\]
Rearranjando os termos, obteremos:
\[dx = dt\left( {{v_0} + at} \right)\]
Agora, integrando e resolvendo a equação acima, obteremos:
\[\int\limits_{{x_0}}^x {dx} = \int\limits_0^t {\left( {{v_0} + at} \right)} dt\]
\[x - {x_0} = {v_0}t + \frac{1}{2}a{t^2}\]
\[\therefore x = {x_0} + {v_0}t + \frac{1}{2}a{t^2} ^{ (13.10)}\]
Vamos utilizar agora a equação 13.6:
\[a = v\frac{{dv}}{{dx}}\]
Uma vez que a aceleração é constante, podemos rearranjar os termos desta equação da seguinte maneira:
\[adx = vdv\]
Assim, podemos integrar esta equação:
\[a\int\limits_{{x_0}}^x {dx} = \int\limits_{{v_0}}^v {vdv} \]
\[a(x - {x_0}) = \frac{1}{2}\left( {{v^2} - v_0^2} \right)\]
\[\therefore {v^2} = v_0^2 + 2a(x - {x_0}) ^{ (13.11)}\]
A equação 13.11 é conhecida como equação de Torricelli. Vele ressaltar que as equações 13.9, 13.10 e 13.11 somente poderão ser utilizadas quando o móvel possuir uma aceleração constante.

Para aprofundar mais sobre o MRUV e encontrar alguns exercícios, eu recomendo a apresentação:
O Movimento Retilíneo Uniformemente
Variado (MRUV).
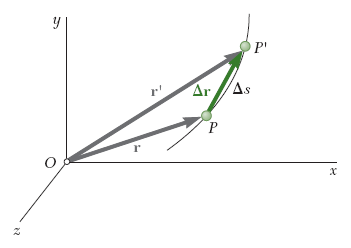
Quando um móvel se desloca ao longo de uma curva, dizemos se tratar de um movimento curvilíneo e, assim, temos de definir outra maneira para determinar a posição P de um móvel. A figura 2 mostra um sistema de coordenadas cartesiano com uma origem O onde o vetor r sai da origem O e vai até a posição P de um móvel ao longo do espaço. O vetor r é chamado de vetor posição do móvel no instante t.
A velocidade instantânea é definida em termos do vetor posição r através da seguinte
relação:
\[v = \mathop {\lim }\limits_{\Delta t \to 0} \frac{{\Delta r}}{{\Delta t}} = \frac{{dr}}{{dt}} ^{ (13.12)}\]
Desse modo, também podemos definir a aceleração instantânea:
\[a = \mathop {\lim }\limits_{\Delta t \to 0} \frac{{\Delta v}}{{\Delta t}} = \frac{{dv}}{{dt}} ^{ (13.13)}\]
A velocidade de um móvel é um vetor tangente à trajetória desse móvel, entretanto, em geral, a aceleração não é tangente a essa trajetória.
Portanto, torna-se necessário decompor a aceleração em componentes ao longo da tangente e da normal à trajetória da partícula.
Dessa maneira, podemos definir dois vetores unitários \({e_n}\) e \({e_t}\) ao longo da reta normal à trajetória de um móvel e ao longo da reta tangente à trajetória respectivamente (Figura 3).

Podemos mostrar que:
\[{e_n} = \frac{{d{e_t}}}{{d\theta }} ^{ (13.14)}\]
Apesar de que a demonstração da equação 13.14 não foi mostrada aqui, esta equação é bastante importante e deverá ser decorada.
Já sabemos que a velocidade de um móvel é tangente à trajetória e pode ser expressa da seguinte maneira.
\[v = v{e_t} ^{ (13.15)}\]
Para obtermos a aceleração a partir da velocidade expressa na equação 13.15, precisamos realizar uma derivada em relação ao tempo:
\[a = \frac{{dv}}{{dt}} = \frac{d}{{dt}}\left( {v{e_t}} \right) = \frac{{dv}}{{dt}}{e_t} + v\frac{{d{e_t}}}{{dt}} ^{ (13.16)}\]
Utilizando a regra da cadeia, podemos chegar à seguinte relação:
\[\frac{{d{e_t}}}{{dt}} = \frac{{d{e_t}}}{{d\theta }}\frac{{d\theta }}{{ds}}\frac{{ds}}{{dt}} { (13.17)}\]
Lembrando que \(\frac{{ds}}{{dt}} = v\), \(\frac{{d\theta }}{{ds}} = \frac{1}{\rho }\) onde \(\rho \( é o raio de curvatura da trajetória em P (Figura 4) e, usando a equação 13.14, podemos chegar em:
\[\frac{{d{e_t}}}{{dt}} = \frac{v}{\rho }{e_n} ^{ (13.18)}\]
E, substituindo o resultado de 13.18 na equação 13.18 obteremos a seguinte expressão:
\[a = \frac{{dv}}{{dt}}{e_t} + \frac{{{v^2}}}{\rho }{e_n} ^{ (13.19)}\]
A equação 13.19 decompõe a aceleração nas direções normal e tangencial da trajetória de um corpo em movimento curvilíneo. O primeiro termo do lado direito desta equação é chamado de aceleração tangencial enquanto que o segundo termo é chamado de aceleração centrípeta que aponta para o centro da trajetória curvilínea.

Em alguns problemas em engenharia, é necessário utilizar as coordenadas polares \(r\) e \(\theta \) para facilitar sua a resolução. Assim, de maneira similar a que fizemos na seção anterior, vamos decompor a velocidade e a aceleração em termos de componentes radial e transversal (Figura5).

Podemos demonstrar que \(\frac{{d{e_r}}}{{d\theta }} = {e_\theta }\) e \(\frac{{d{e_\theta }}}{{d\theta }} = - {e_r}\) e escrevendo o vetor posição como um produto:
\[r = r{e_r} ^{ (13.20)}\]
Derivando uma e duas vezes, obteremos as equações de velocidade e aceleração, escritas aqui sem demonstração:
\[v = \dot r{e_r} + r\dot \theta {e_\theta } ^{(13.21)}\]
E:
\[a = \left( {\ddot r - r{{\dot \theta }^2}} \right){e_r} + \left( {r\ddot \theta + 2\dot r\dot \theta } \right){e_\theta
} ^{ (13.22)}\]
Dessa maneira, conseguimos decompor a velocidade e a aceleração em componentes radial e traDnsversal. As equações 13.20, 13.21 e 13.22 são principais para problemas em coordenadas polares.

Para maiores detalhes sobre movimentos retilíneos e curvilíneos eu recomendo o link:
Mecânica I | Movimento curvilíneo: componentes cilíndricas
Aula Concluída!
Avançar