Um sistema de forças planares atuando em uma estrutura rígida sempre pode ser reduzido a duas forças resultantes:
Pela segunda lei de Newton, a aceleração linear a do centro de gravidade e as acelerações angulares do corpo sobre o centro de gravidade são relativas às forças resultantes R e M. Se o corpo está em repouso — o que é denominado estado de equilíbrio estático —, tanto a aceleração linear a quanto a aceleração angular são iguais a zero.
Se R for substituída por suas componentes Rx e Ry, que podem ser expressas relativamente às componentes do sistema de forças reais, podemos escrever as equações de equilíbrio estático para um sistema de forças planar como:
\[\sum F_{x} = 0\\ \sum F_{y}= 0 \\ \sum M_{z} = 0\]
Se as forças que atuam em uma estrutura — incluindo as reações e as forças internas — podem ser calculadas usando qualquer um dos conjuntos de equações de equilíbrio estático anteriores, diz-se que a estrutura é estaticamente determinada ou, mais simplesmente, determinada.
Se a estrutura é estável, mas as equações de equilíbrio não fornecem equações suficientes para analisá-la, é chamada indeterminada. Para analisar estruturas indeterminadas devemos derivar equações adicionais a partir da geometria da estrutura deformada, para complementar as equações de equilíbrio.
As reações de muitas estruturas podem ser determinadas tratando a estrutura como um único corpo rígido. Outras estruturas determinadas estáveis, compostas de vários elementos rígidos conectados por meio de uma articulação ou que contêm outros dispositivos ou condições de construção que liberam certas restrições internas, exigem que a estrutura seja dividida em vários corpos rígidos para se avaliarem as reações. Poderíamos determinar as reações nos apoios e as forças na articulação central escrevendo e resolvendo três equações de equilíbrio. Considerando os dois corpos livres, temos seis equações de equilíbrio disponíveis para resolver, para seis forças desconhecidas.

Calcule as reações da viga. (Leet, Kenneth M., 2009, pg.90).

Devemos decompor a força C nas componentes.
\[\sum F_{x} = 0 \rightarrow A_{x} + 6 = 0 \rightarrow A_{x} = -6\\ \sum F_{y}= 0 \rightarrow A_{y} + B_{y} - 8 = 0 \rightarrow = -4Kips\\ \sum M_{z} = 0 \rightarrow -10B_{y} + 8(15) = 0 \rightarrow B_{y} = 12Kips\]
O sinal positivo indica que a direção do vetor assumida está correta e o sinal menos indica que a direção assumida está incorreta e a reação deverá ser invertida. Observe as figuras:



Calcule as reações para a treliça (Leet, Kenneth M., 2009, pg.91):
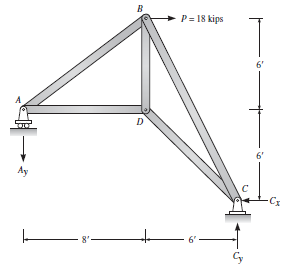
\[ \mathop{\sum }^{}{{M}_{c}}=0\to 18\left( 12 \right)-{{A}_{y}}\left( 14 \right)=0\to {{A}_{y}}=15,42Kips \\ \mathop{\sum }^{}{{F}_{x}}=0~\to -18-~{{C}_{x}}\to {{A}_{x}}=0~\to {{C}_{x}}=18Kips \\ \mathop{\sum }^{}{{F}_{y}}=0~\to -{{A}_{y}}+{{C}_{y}}=0~\to {{C}_{y}}=15,43~Kips~\]


Calcule as reações da viga (Leet, Kenneth M., 2009, pg.95).

Os apoios da estrutura fornecem quatro reações. Usando as três equações de equilíbrio da estática e considerando que articulação em C fornece mais uma equação de equilíbrio, a estrutura é considerada determinada. Vamos calcular o Ey somando os momentos sobre C:
\[\mathop{\sum }^{}{{M}_{c}}=0\to 24\left( 5 \right)-{{E}_{y}}\left( 10 \right)\to {{E}_{y}}=12Kips \\ \mathop{\sum }^{}{{F}_{x}}=0\text{ }\!\!~\!\!\text{ }\to 0+\text{ }\!\!~\!\!\text{ }{{E}_{x}}=0\to {{E}_{x}}=0\text{ }\!\!~\!\!\text{ } \\ \mathop{\sum }^{}{{M}_{\text{A}}}=0\to +12\left( 15 \right)+24\left( 20 \right)-{{B}_{y}}\left( 10 \right)\to {{B}_{y}}=36Kips \\ \mathop{\sum }^{}{{F}_{y}}=0\text{ }\!\!~\!\!\text{ }\to -{{A}_{y}}+{{B}_{y}}-12-24+{{E}_{y}}=0\text{ }\!\!~\!\!\text{ }\to {{A}_{y}}=-12\text{ }\!\!~\!\!\text{ }Kips\text{ }\!\!~\!\!\text{ }\]


Calcule as reações na via abaixo(Leet, Kenneth M., 2009, pg.96):


Separando a estrutura em dois corpos livres podemos ter 6 equações de equilíbrio (3 para cada corpo) para determinar as 6 reações que surgiram na estrutura através das reações.
\[\mathop{\sum }^{}{{F}_{x}}=0\text{ }\!\!~\!\!\text{ }\to 15-\text{ }\!\!~\!\!\text{ }{{D}_{x}}=0\text{ }\!\!~\!\!\text{ }\to {{D}_{x}}=15\text{ }\!\!~\!\!\text{ }kips \\ \mathop{\sum }^{}{{M}_{D}}=0\to 0={{B}_{y}}\left( 10 \right)-20\left( 5 \right)\to
{{B}_{y}}=10Kips \\ \mathop{\sum }^{}{{F}_{y}}=0\text{
}\!\!~\!\!\text{ }\to 0={{B}_{y}}-20+{{D}_{y}}=0\text{ }\!\!~\!\!\text{ }\to
{{D}_{y}}=10Kips\text{ }\!\!~\!\!\text{ } \\ \mathop{\sum
}^{}{{F}_{x}}=0\text{ }\!\!~\!\!\text{ }\to {{A}_{x}}=0 \\ \mathop{\sum
}^{}{{M}_{A}}=0\to 0=10\left( 10 \right)-15{{C}_{y}}\to {{C}_{y}}=20/3Kips \\ \mathop{\sum }^{}{{F}_{y}}=0\text{ }\!\!~\!\!\text{ }\to 0={{A}_{y}}-10+{{C}_{y}}=0\text{
}\!\!~\!\!\text{ }\to {{A}_{y}}=10/3Kips\text{ }\!\!~\!\!\text{ }\]

Uma estrutura está restringida quando possui vínculos para restringir todos os movimentos possíveis da estrutura (translação e rotação) como um corpo rígido.

Observe as vigas abaixo:

Quantidade de apoio: \({{c}_{1}}=3\)
Número de Barras: \(m=1\)
\[{{g}_{h}}={{c}_{1}}+2\text{*}{{c}_{2}}+3\text{*}{{c}_{3}}-3\text{*}m \\ {{g}_{h}}=\left( 3 \right)+2\text{*}\left( 0 \right)+3\text{*}\left( 0 \right)-3\text{*}1 \\ {{g}_{h}}=\left( 3 \right)-\left( 3 \right)\to {{g}_{h}}=0\]

Quantidade de apoio: \({{c}_{1}}=2\text{ }\!\!~\!\!\text{ }\!\!~\!\!\text{ }\!\!~\!\!\text{ }\!\!~\!\!\text{ }\!\!~\!\!\text{ }\!\!~\!\!\text{ }{{c}_{2}}=1\)
Número de Barras: \(m=2\)
Ligações internas:
\[C_{2}=2-1=1 \text{ a rótula interna é uma conexão } C_{2} \\ g_{h}= c_{1}+2*c_{2}+3*c_{3}-3*m \\ g_{h}= \left( 2\right)+2*\left( 2\right)+3*\left( 0\right)-3*\left( 2\right) \\ g_{h}= \left( 2\right)+\left( 4\right)-\left( 6\right)\rightarrow g_{h}=0\]

Quantidade de apoio: \({{c}_{1}}=1~~~~~~{{c}_{2}}=1\)
Número de Barras: \(m=3\)
Ligações internas:
\[{{c}_{2}}=2-1=1~ \\ {{c}_{3}}=2-1=1 \\ {{g}_{h}}={{c}_{1}}+2*{{c}_{2}}+3*{{c}_{3}}-3*m \\ {{g}_{h}}=\left( 1 \right)+2*\left( 2 \right)+3*\left( 1 \right)-3*\left( 3 \right) \\ {{g}_{h}}=\left( 1 \right)+\left( 4 \right)+\left( 3 \right)-\left( 9 \right)\to {{g}_{h}}=-1\]
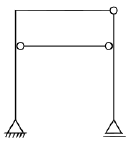
Quantidade de apoio: \({{c}_{1}}=1~~~~~~{{c}_{2}}=1\)
Número de Barras: \(m=3\)
Ligações internas:
\[{{c}_{1}}=2-1=1~ \\ {{c}_{2}}=2-1=1 \\ {{c}_{3}}=2-1=1 \\ {{g}_{h}}={{c}_{1}}+2*{{c}_{2}}+3*{{c}_{3}}-3*m \\ {{g}_{h}}=\left( 2 \right)+2*\left( 2 \right)+3*\left( 1 \right)-3*\left( 3 \right) \\ {{g}_{h}}=\left( 2 \right)+\left( 4 \right)+\left( 3 \right)-\left( 9 \right)\to {{g}_{h}}=0\]

Quantidade de apoio: \({{c}_{2}}=1~~~~~~{{c}_{3}}=1\)
Número de Barras:
\[m=1 \\ {{g}_{h}}={{c}_{1}}+2*{{c}_{2}}+3*{{c}_{3}}-3*m \\ {{g}_{h}}=\left( 0 \right)+2*\left( 1 \right)+3*\left( 1 \right)-3*\left( 1 \right) \\ {{g}_{h}}=\left( 2 \right)+\left( 3 \right)-\left( 3 \right)\to {{g}_{h}}=2\]

A partir deste modelo podemos notar que o g_i de uma estrutura fechada é igual a 3 independente da forma geométrica
\[{{g}_{h}}={{c}_{1}}+2*{{c}_{2}}+3*{{c}_{3}}-3*m \\ {{g}_{h}}=\left( 1 \right)+2*\left( 1 \right)+3*\left( 4 \right)-3*\left( 4 \right) \\ {{g}_{h}}=\left( 1 \right)+\left( 2 \right)+\left( 12 \right)-12\to {{g}_{h}}=3 \\ {{g}_{e}}={{c}_{1}}+2*{{c}_{2}}+3*{{c}_{3}}-3 \\ {{g}_{e}}=\left( 1 \right)+2-3 \\ {{g}_{e}}=0 \\ {{g}_{h}}={{g}_{e}}+{{g}_{I}} \\ \left( 3 \right)=\left( 0 \right)+{{g}_{I}} \\ {{g}_{i}}=3\]

Aula Concluída!
Avançar