| Unidade 1 -
Estudantes, vamos agora estudar o conceito de equilíbrio de um ponto material. Os conceitos apreendidos aqui têm grande valia para a formação nessa área. Continue estudando!
Da primeira lei de Newton, sabemos que, para um corpo estar em equilíbrio, ele deverá estar em repouso ou em movimento retilíneo uniforme. Mais frequentemente em estática, utilizamos a palavra equilíbrio para descrever objetos em repouso. Desse modo, para manter um corpo em repouso, a primeira lei de Newton deve ser satisfeita, ou seja, a força resultante que atua num objeto deve ser nula. Matematicamente, escrevemos:
\[\sum {F} = {0} ~~~~~~~ (1.1) \]
Onde \(\sum {F}\) representa todas as forças que atuam sobre o objeto.
A equação 3.1 é uma condição necessária e suficiente para se alcançar o equilíbrio estático. É interessante notar que essa condição decorre da segunda lei de Newton, o princípio fundamental da dinâmica \(\sum {F} = m{a}\). Na condição da equação 3.1, podemos escrever \( m {a} = \overrightarrow{0}\) e, dessa maneira, a aceleração do objeto deve ser nula \( {a} = {0}\). Portanto, para que a aceleração do ponto material seja nula, este permanece em repouso ou em movimento retilíneo uniforme.
Para aplicarmos a condição de equilíbrio, devemos primeiramente determinar todas as forças que atuam sobre um ponto material \(\sum {F} \), sejam elas conhecidas e desconhecidas. Uma maneira de simplificarmos essa tarefa é elaborar um diagrama de corpo livre do ponto material. Um diagrama é um esboço, um “desenho” onde representaremos o objeto analisado como um “ponto” isolado de todo o universo em volta dele juntamente com todas as forças que atuam sobre ele. Na nossa segunda videoaula desta unidade, mostraremos o passo a passo para se elaborar corretamente um diagrama de corpo livre. Vale a pena conferir!
Veremos agora três tipos de conexões que são encontradas nos problemas relacionados à mecânica. São as molas, os cabos e as polias.
As molas são objetos que se deformam quando submetidas à ação de uma força. Essa força é diretamente proporcional à variação de comprimento da mola. Uma mola é caracterizada por sua constante da mola ou rigidez da mola simbolizada por “k”. Quanto mais rígida a mola, maior o valor da constante da mola e vice-versa. Denotaremos a deformação sofrida pela mola por “s”. A intensidade da força da mola é dada pela lei de Hooke:
\[F= ks ~~~~~~~ (1.2)\]
A deformação s é medida pela diferença de comprimento da mola deformada l e o comprimento da mola sem deformação l0. Logo \( s= l-l_{0}\), veja a figura.
Os cabos e as polias são frequentemente utilizados em conjunto. Ao longo dessa obra, vamos considerar que todos os cabos e/ou cordas possuam peso desprezível e são indeformáveis. A força que atua num cabo é chamada de tensão ou tração. Essa força atua sempre na direção do cabo. Dessa forma, para qualquer inclinação, como mostrada na figura a seguir, o cabo está submetido a uma tensão T ao longo de seu comprimento.
Se um objeto estiver sob a ação de um sistema de forças bidimensionais, ou seja, forças coplanares (suponha no plano xy), então, as forças envolvidas podem ser decompostas nas direções dos vetores unitários \(\hat i\) e \(\hat j\). Dessa maneira, a condição de equilíbrio fica:
\(\sum\overrightarrow{F}=\overrightarrow{0} \\ \sum F_{x}\widehat{i}=\sum F_{x}\widehat{j}=\overrightarrow{0}\)
A equação acima representa uma equação vetorial e, para que ela seja satisfeita, devemos ter:
\(\sum F_{x}=0\ \\ \sum F_{x}=0~~~~~~~(1.3)\)
Essas são as condições de equilíbrio para um sistema de forças bidimensionais.
As equações 3.3 requerem que as somas algébricas das componentes x e y de todas as forças que atuam sobre um ponto material seja nula. Como elas representam um sistema de duas equações, somente são resolvidas para no máximo duas incógnitas.
Exemplo 3.1
Solução:
A solução deste tipo de problema se resume a dois passos importantes: elaboração de um diagrama de corpo livre e aplicação das condições de equilíbrio.
Vamos ao passo inicial: a ideia fundamental aqui é relacionar as tensões nos cabos com algum ponto material da figura. Começamos pelo anel em A, pois esse corpo está submetido tanto à tração no cabo \(\overline{AB}\) quanto ao cabo \(\overline{AD}\). É conhecido o peso do objeto \(w=(250kg)\cdot(9,81m/s^2)=2,452kN\)que é sustentado pelo cabo \(\overline{AC}\). Dessa maneira, para o ponto material escolhido, o anel A, existem três forças atuando. Vamos nomeá-las: \(\overrightarrow{T}_b\)a tração no cabo \(\overline{AB}\), \(\overrightarrow{T}_d\) a tração no cabo \(\overline{AD}\) e a força peso \(\overrightarrow{w}\). Portanto, duas forças desconhecidas e uma conhecida. Dessa maneira, o diagrama de corpo livre para o anel A fica:
Agora, para aplicarmos a condição de equilíbrio, utilizaremos as equações 3.3, \(\sum F_x=0 \)e \(\sum F_y=0 \). Para isso, devemos decompor a tração \(\overrightarrow{T}_b\) em suas componentes nos eixos x e y.
Logo:
Resolvendo a equação (ii) para TB e substituindo na equação (i) para encontrar TD, temos:
Já sabemos que, para que um ponto material esteja em equilíbrio, devemos ter \[\sum \overrightarrow{F}=\overrightarrow{0}\]Se por ventura as forças que atuam nesse corpo puderem ser decompostas em suas componentes nas direções x, y e z, obtemos:
\[\sum {F_x}\widehat{i}+\sum {F_y}\widehat{j}+\sum {F_z}\widehat{k}=\overrightarrow{0}~~~~~~~(1.4)\]
Dessa forma, o equilíbrio é satisfeito se:
\[\sum {F_x}=0\] \[\sum {F_y}=0\] \[\sum {F_z}=0~~~~~~~~~(1.5)\]
Da mesma maneira que em 2D, as equações 3.5 são equações algébricas e correspondem a um sistema de três equações que possui solução com até três incógnitas.
O passo a passo para resolução dos problemas em 3D requer apenas a adição de mais uma componente nas equações de condição de equilíbrio. Para que os estudantes possam verificar como se aplicam essas condições, eu recomendo o seguinte link
Mecânica Técnica.
Primeiramente, devemos ter em mente que o momento da força é o torque já trabalhado e conhecido da disciplina Física 2. O momento de uma força é definido em relação de um ponto ou a um eixo e fornece a medida da tendência dessa força de realizar uma rotação de um corpo em relação a um ponto ou a um eixo. Podemos citar como exemplo a força F representada na figura seguinte aplicada na extremidade de uma barra delgada. Pela posição onde a força está sendo aplicada, ela pode provocar uma rotação no sentido indicado pela seta escura curvada no centro da figura. Geralmente, indicamos o sentido de rotação anti-horária como sendo o sentido de rotação positiva. Verificamos também que a força aplicada tende a provocar um giro em relação ao eixo z indicado para fora do plano do papel não mostrado na figura. Quanto maior a distância d de aplicação da força em relação ao centro O, maior o efeito de rotação.
Denotamos o momento da força indicada na Figura 17 por M\(_{O}\), que indica que o sentido de rotação da força é em relação ao ponto O. Ainda poderíamos indicar esse momento por (M\(_{O}\))\(_{z}\) para indicar que a rotação ocorre em torno do eixo z.
Vamos agora considerar o exemplo da Figura 18, no qual uma força é aplicada na extremidade de um disco. O momento M\(_{O}\) em relação ao ponto O ou em relação a um eixo que passa por O perpendicularmente ao plano é uma quantidade vetorial e, portanto, devemos usar todo o formalismo por trás do espaço vetorial para trabalharmos com o momento da força. Assim, se o M\(_{O}\) é um vetor, este deverá ter módulo, direção e sentido.
Sua intensidade é dada por:
\[M_o=Fd~~~~~~~(1.6)\]
Onde d é chamando de braço de alavanca ou braço do momento e é a distância perpendicular do ponto O até a linha de ação da força (a linha onde a força está sendo aplicada) Figura 18. No SI, a unidade de medida do momento da força é o \(N\cdot m\)
A direção e o sentido do momento da força são dados pela regra da mão direita. Para aplicar essa regra, curve os dedos da mão direita no sentido de rotação da força como indicado na figura anterior. O polegar se orienta ao longo do eixo do momento, determinando, assim, a direção e o sentido do vetor momento. No caso da Figura 18, o vetor momento está dirigido para cima e é perpendicular ao plano que contém F e d.
Como o momento da força é uma quantidade vetorial e é definida em três dimensões, precisamos retomar nossos conhecimentos sobre álgebra vetorial.
Sejam dois vetores A e B. O produto vetorial entre A e B produz um terceiro vetor C perpendicular ao plano que contém os vetores A e B, como na Figura 19. Matematicamente, representamos o produto vetorial por:
\[\overrightarrow{A}\times\overrightarrow{B}=\overrightarrow{C}~~~~~~~~~(3.7)\]
A intensidade do vetor C é dada por:
\[C= ABsen\theta~~~~~~~(1.8)\]
Onde é o ângulo entre os vetores A e B, enquanto a direção e o sentido são dados pela regra da mão direita do produto vetorial indicado na figura anterior.
Uma das propriedades mais importantes do produto vetorial é a não comutatividade, ou seja:
\[\overrightarrow{A}\times\overrightarrow{B}\neq\overrightarrow{B}\times\overrightarrow{A}~~~~~~~~~(3.9)\]
Essa propriedade pode ser facilmente verificada na Figura 20.
Para revisar melhor os conceitos por trás do produto vetorial, eu recomendo o link a seguir.
Produto Vetorial.
A formulação vetorial serve pra generalizar a definição do momento da força. Assim, o momento da força F\(_{em}\) relação ao ponto O ou em relação a um eixo que passa por O perpendicularmente ao plano que contém O e F (Figura 21) é dado por:
\[\overrightarrow{M_o}=\overrightarrow{r}\times\overrightarrow{F}~~~~~~~~~(1.10)\]
Assim, o vetor representa o vetor posição traçado de O até qualquer ponto sobre a linha de ação da força. A intensidade do produto vetorial definido na equação 4.5 é dada por:
\[M_o = rFsen\theta~~~~~~~(1.11)\]
Onde o ângulo q é medido entre r e F (Figura 21). Podemos ver claramente na Figura 21 que \(d=rsen\theta\). Logo:
\[M_o = rFsen\theta=F(rsen\theta)=Fd\]
O que está em perfeito acordo com a equação 4.1.
O princípio dos momentos (também chamado de teorema de Varignon) estabelece que momento de uma força em relação a um ponto é igual à soma dos momentos dos componentes das forças em relação ao mesmo ponto. Para verificarmos esse princípio, aplicamos a propriedade distributiva do produto vetorial.
Considere que a força F seja decomposta em suas componentes retangulares F\(_{1}\) e F\(_{2}\), como indica a Figura 22. Então, teremos:
\[A\times \overrightarrow{B}\neq B\times \overrightarrow{A}~~~~~~~(1.12)\]
Esse teorema será bastante útil na resolução de vários problemas em estática, como veremos no exemplo a seguir.
Às vezes, queremos encontrar a componente do vetor momento de uma força em relação a um determinado eixo específico. Vamos abordar o problema da maneira mais fácil para facilitar o entendimento do leitor. Considere a Figura 23.
A estrutura tubular se estende no plano horizontal e está sujeita a uma força vertical de 20 N aplicada sobre o ponto A. O momento dessa força em relação ao ponto O tem intensidade\[Mo=(20N)(0,5 m)=10N\cdot m\]e direção e sentido dados pela regra da mão direita, como indica a Figura 23. Podemos observar que esse momento tende a rotacionar o tubo em relação ao eixo Ob. Vamos, então, determinar a componente de M\(_{O}\) em relação ao eixo y, M\(_{y}\), pois essa componente tende a desparafusar o tubo da flange em O. Da figura, é fácil verificar que a componente M\(_{y}\) tem intensidade \(M_y=\frac{3}{5}(10N\cdot m)=6N\cdot m\) e a direção e sentido são apresentados pelos vetores indicados na figura.
Um binário é composto por duas forças paralelas separadas por uma distância d, de mesma intensidade, mas de sentidos opostos, como indica a Figura 24. Como a força resultante é nula, temos como único efeito a rotação.
Essa rotação ou tendência de rotação que existe num binário é chamada de momento de um binário. Pode-se obter seu valor calculando a soma dos momentos das forças que compõem o binário em relação a um ponto arbitrário qualquer. Tome, por exemplo, a figura a seguir, os vetores r\(_{A}\) e r\(_{B}\) orientados do ponto O para os pontos A e B, onde se aplicam as forças F e -F.
Figura 25. Binário
O momento desse binário é:
\[M=R_{a}\times(-F)+r_b\times F\]
Podemos realizar um procedimento alternativo, mais simples. Para determinar o momento do binário, escolhemos um ponto localizado na linha de ação das forças, por exemplo, o ponto A. Nesse caso, o momento de é -F nulo. Portanto:
\[M=r\times F~~~~~~~(1.13) \]
Para mais exemplos, aplicações e cálculos de momentos de força acesse o link a seguir. Neste, o estudante encontrará um resumo sobre momento de força e várias aplicações práticas.
Mecânica Técnica Aula 11.
Vimos até agora que uma força aplicada sobre um corpo tem a capacidade de tanto fazê-lo transladar quanto de rotacionar. Veremos, na última seção desta aula, que é possível substituir um sistema de forças e momentos de binário por um sistema com uma única força e momento de binário. Esse recurso somente será possível se o sistema de forças e momentos de binário produzir o mesmo efeito externo de translação e rotação de um corpo.
Vamos mostrar isso em um exemplo concreto. Considere um corpo qualquer, como na Figura 26(a), sujeito a uma força F aplicada no ponto A. Nossa intenção é aplicar a força F no ponto O, entretanto, sem modificar os efeitos externos dessa força sobre o corpo. Para isso, aplicamos as forças F e -F como indicado na Figura 26(b). A força F aplicada ao ponto A se anula com a força -F aplicada no ponto O por serem opostas de mesma direção e intensidade. O que resta é apenas a força F aplicada ao ponto O, Figura 26(c).
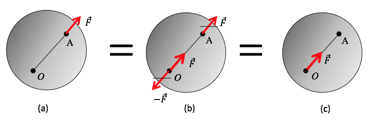
Esse é procedimento realizado para obtenção de um sistema equivalente. Observe que a força foi “deslocada” ao longo da linha de ação da força, do ponto A para o ponto O.
O procedimento realizado na seção anterior é extremamente útil na análise de um corpo rígido sujeito a um sistema de forças e momentos de binários, onde substituímos o sistema por um equivalente com uma única força resultante, atuando num ponto qualquer e um momento resultante.
Mais uma vez vamos recorrer a um caso concreto para exemplificar essa técnica. Considere a Figura 27. É fácil verificar que o ponto O não está localizado sobre a linha de ação das forças F\(_{1}\) e F\(_{2}\), Figura 27(a), assim, podemos deslocá-las para O, bem como considerar os seus respectivos momentos M\(_{1}\) e M\(_{2}\), Figura 27(b). Finalmente, consideraremos apenas os efeitos de uma força resultante F\(_{R}\) e de um momento resultante M\(_{R}\), Figura 27(c).
Tal procedimento nos permite obter uma resultante de sistemas de forças e momentos de binários e que pode ser representado pelas seguintes equações:
\[F_r= \sum F\]
\[M_r= \sum M_c+ \sum M_o\]
Aula Concluída!
Avançar