Aqui vamos entender que análise estrutural é a etapa do projeto estrutural na qual é feita uma previsão do comportamento da estrutura. Todas as teorias físicas e matemáticas resultantes da formalização da Engenharia Estrutural como ciência são utilizadas na análise estrutural (Martha, 2008, p. 3).
O modelo utilizado para representar matematicamente uma estrutura é chamado de modelo estrutural e incorpora todas as teorias e hipóteses possíveis para descrever o comportamento da estrutura para as diversas solicitações que poderá estar submetida. Essas hipóteses são baseadas em leis físicas, tais como o equilíbrio entre forças e entre tensões, as relações de compatibilidade entre deslocamentos e deformações, e as leis constitutivas dos materiais que compõem a estrutura (Martha, 2008, p. 3).
A criação do modelo estrutural de uma estrutura real é uma das tarefas mais importantes da análise estrutural. Essa tarefa pode ser bastante complexa, dependendo do tipo de estrutura como. O modelo estrutural de um prédio residencial de pequeno porte é formado por um conjunto de linhas que representam as vigas e colunas do prédio e pelas superfícies que representam as lajes de seus pavimentos.
As estruturas se compõem de uma ou mais peças ligadas entre si ao meio exterior de modo a formar um conjunto estável, isto é, um conjunto capaz de receber solicitações externas, absorvê-las internamente e transmiti-las até seus apoios, onde estas solicitações externas encontrarão seu sistema estático equilibrante (Sussekind, 1981, p. 1)
Baseado no conceito de estruturas passamos ao próximo conceito necessário para o bom entendimento deste curso, como conceito de concepção estrutural. Na concepção do modelo estrutural é feita uma idealização do comportamento da estrutura real em que se adota uma série de hipóteses simplificadoras. Estas estão baseadas em teorias físicas e em resultados experimentais e estatísticos, e podem ser divididas nos seguintes tipos (Martha, 2008, p. 4):
Abaixo um exemplo de concepção estrutural mostrando uma estrutura real de um galpão com vigas e colunas e uma representação gráfica do mesmo para fins de estudos de análise estrutural:

Podemos definir também a estrutura como um conjunto formado pelas partes resistentes que garantem a estabilidade de um objeto de projeto, por exemplo, uma edificação. Podemos observar também que quando se projeta uma estrutura, a análise do comportamento estrutural exige que sejam feitas algumas simplificações que conduzem a modelos estruturais. Para que se defina o sistema estrutural mais adequado, para uma determinada situação de projeto, devem ser considerados outros vários fatores. Os principais são:
Portanto para identificação do sistema estrutural mais adequado deve-se identificar as possíveis opções e analisar e comparar as vantagens e inconvenientes de cada um.
As estruturas devem ser estáveis sob todas as condições de carregamento; isto é, devem ser capazes de suportar as cargas aplicadas (o próprio peso, as sobrecargas antecipadas, vento etc.) sem mudar de forma, sofrer grandes deslocamentos ou ruir. Como as estruturas estáveis não se movem perceptivelmente quando carregadas, em grande parte sua análise — a determinação das forças internas e externas (reações) — é baseada nos princípios e nas técnicas contidas no ramo da mecânica denominado estática (Leet, Kenneth M., 2009, pg.71).
Embora as estruturas absolutamente rígidas, pois sofrem pequenas deformações elásticas quando carregadas, na maioria das situações as deflexões são tão pequenas que podemos:
Estruturas que não pode ser analisada pelas equações da estática são denominadas estruturas indeterminadas.
Para analisar uma estrutura indeterminada, devemos fornecer equações adicionais, considerando a geometria da forma defletida. Essas estruturas serão aplicadas e ensinadas em conteúdos e disciplinas posteriores a esta.
Por estabilidade, referimo-nos à organização geométrica dos membros e apoios necessários para produzir uma estrutura estável; isto é, uma estrutura que possa resistir à carga de qualquer direção sem sofrer uma mudança radical no formato ou grandes deslocamentos de corpo rígido. Consideraremos a estabilidade e a determinação de estruturas que podem ser tratadas como um único corpo rígido ou como vários corpos rígidos conectados. Os princípios que estabelecermos para essas estruturas simples podem ser ampliados para estruturas mais complexas (Leet, Kenneth M., 2009pg. 71).
Problemas estruturais típicos dentro dos princípios da estática sempre envolverão aplicação de forças e equações que envolverão estas forças e suas componentes. Uma força pode ser linear, se tende a produzir translação, ou um conjugado, se tende a produzir rotação do corpo em que atua. As forças são grandezas vetoriais, caracterizadas por direção, sentido e intensidade. Como força tem magnitude e direção, pode ser representada por um vetor. Por exemplo, a Figura2 mostra uma força F com magnitude F situada no plano xy e passando pelo ponto A. O vetor da força linear está decomposto nas componentes x e y:

O momento M associado ao conjugado é igual ao produto da força F e a distância perpendicular (ou braço) d entre as forças (Figura 3). Como o momento é um vetor, ele tem magnitude, assim como direção. Na regra da mão direita, curvamos os dedos da mão direita na direção do momento, e a direção na qual o polegar aponta indica a direção do vetor. Precisamos muitas vezes efetuar cálculos que exigem decompor uma força em suas componentes ou combinar várias forças para produzir uma única força resultante(Leet, Kenneth M., 2009, pg 75).

Exemplo1 (Leet, Kenneth M., 2009, pg. 76, Exemplo 3.1): Usando a lei dos cossenos, decomponha a força vertical FAB nas componentes:
Os ângulos internos devem ser calculados e posteriormente calcula-se os vetores AC e BC que representam as forças componentes de FAB:
\[F_{AC}=75lb\]


\[\frac{sin80}{75} = \frac {sin40}{F_{AC}} = \frac {sin60}{F_{CB}}\\ F_{AC} = \frac {sin40}{sin80}(75) = 48,96lb\\ F_{CB} = \frac {sin60}{sin80}(75) = 65,94lb\]
Determine o valor e localização da resultante R:
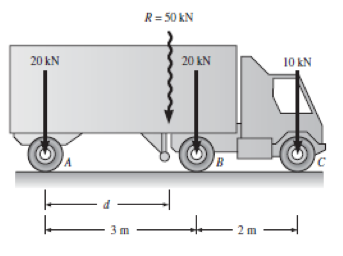
Para determinar a magnitude e a localização da resultante de um sistema de forças, consideraremos que cada resultante é uma força única que produz em um corpo o mesmo efeito externo do sistema de forças original, a resultante R deve satisfazer as três condições a seguir:
\[R_{x} = \sum F_{x}\]
\[R_{y} = \sum F_{y}\]
\[M_{0} = Rd = \sum F_{i}d_{I} + \sum M_{I}\]
\[R = R_{y} = \sum F_{y} = 20 + 20 + 10 = 50kN\\ R_{d} = \sum F_{I}d_{I}500d = 20(0) + 20(3) + 10(5) \rightarrow d = 2,2m\]

Sabia mais!! Leia o livro Análise estrutural e a apostila Análise estrutural I para se inteirar mais sobre esse sobre conteúdo.
Os sistemas estruturais são modelos de comportamento idealizados para representação e análise de uma estrutura tridimensional. Estes modelos obedecem a uma convenção. Esta convenção pode ser feita em função da geometria das peças estruturais que compõem o conjunto denominado sistema estrutural. Quanto à geometria, um corpo pode ser identificado por três dimensões principais que definem seu volume. Conforme as relações entre estas dimensões, surgem quatro tipos de peças estruturais:
Barra: duas dimensões da mesma ordem de grandeza e uma terceira maior que as outras duas.

Barra de elementos delgados: as três dimensões principais são de diferentes ordens de grandeza. É o caso dos perfis metálicos, onde a espessura é muito menor que as dimensões da seção transversal.

Folhas ou lâminas: duas dimensões de mesma ordem de grandeza, maiores que a terceira dimensão. Subdividem-se em:
Placas: carregamento perpendicular ao plano médio.

Chapas: carregamento contido no plano médio.
Cascas: superfície média curva.
Bloco: as três dimensões são da mesma ordem de grandeza, os elementos estruturais combinados irão compor a estrutura como um todo e basearão os sistemas estruturais. Todos os sistemas estruturais são compostos de vários elementos estruturais básicos — vigas, colunas, tirantes, treliças e outros. Vamos descrever as principais características desses elementos básicos:

Tirantes (Leet, Kenneth M., 2009, pg. 10): barras axialmente carregadas em tração de modo uniforme. A capacidade de tencionar membros é uma função direta da resistência à tração do material. Quando as barras são construídas de materiais com alta resistência, como as ligas de aço, têm capacidade de suportar cargas grandes.

Colunas: barras axialmente carregadas em compressão. A capacidade de uma coluna esbelta depende da contenção fornecida em suas extremidades. As colunas transmitem carga axial e momento fletor. Esses membros são chamados de vigas-colunas.

Vigas: As vigas são membros delgados carregados perpendicularmente ao seu eixo longitudinal. As tensões de flexão são diretamente proporcionais ao momento fletor e variam em amplitude ao longo do eixo da viga.

Treliças planas: possui todos os membros axialmente carregados Treliça é um elemento estrutural composto de barras delgadas cujas extremidades são supostamente conectadas por articulações sem atrito.

Pórticos: solicitados por carga axial e momento. As barras de um pórtico rígido, que normalmente suportam carga axial e momento, são chamadas de vigas-pilares.

Lajes: carga transmitida por flexão. As placas são elementos planares cuja profundidade (ou espessura) é pequena, comparada ao comprimento e à largura.

Cargas concentradas são uma forma aproximada de tratar cargas distribuídas aplicadas em áreas pequenas (em presença das dimensões da estrutura), que podem ser consideradas nulas.

Carga aplicada na extensão de uma área da estrutura. A magnitude da resultante de uma carga distribuída é igual à área sob a curva de carga e atua em seu centroide. Se o formato de uma carga distribuída é complexo, muitas vezes o projetista pode simplificar o cálculo da magnitude e da posição da resultante subdividindo a área em várias áreas geométricas menores, cujas propriedades são conhecidas.

Os esforços internos nestes tipos de estrutura não variam apenas com a magnitude das cargas aplicadas, mas também com a posição de atuação das mesmas. Portanto, o projeto de um elemento estrutural, como uma viga de ponte, envolve a determinação das posições das cargas móveis que produzem valores extremos dos esforços nas seções do elemento.
Vínculos são elementos que impedem o deslocamento de pontos das peças, introduzindo esforços nesses pontos correspondentes aos deslocamentos impedidos. Os deslocamentos podem ser de translação ou de rotação. No espaço uma translação pode ser expressa por suas componentes segundo 3 eixos triortogonais e, uma rotação, dizemos que uma estrutura no espaço possui um total de 6 graus de liberdade ( 3 translações e 3 rotações)
Esses 6 graus de liberdade precisam ser restringidos[1] de modo a evitar toda tendência de movimento da estrutura, a fim de ser possível seu equilíbrio. Esta restrição é dada por apoios, que devem impedir as diversas possibilidades de movimentos da estrutura, através do aparecimento de reações destes apoios sobre a estrutura nas direções dos movimentos que foram impedidos.

Apoio simples ou de primeiro gênero

Reação aparece na direção do movimento impedido.

Rótula ou apoio do segundo gênero


As vigas representam um dos elementos mais comuns encontrados em estruturas. Quando uma viga é carregada perpendicularmente ao seu eixo longitudinal, forças internas — cortante e momento — desenvolvem- se para transmitir as cargas aplicadas para os apoios.
Uma viga apoiada por uma articulação fixa em uma extremidade e por uma articulação móvel na outra extremidade é chamada viga com apoio simples (a). Se a extremidade com apoio simples se estende sobre um apoio, denomina-se viga em balanço (b). Uma viga em balanço é fixa em uma extremidade, contra translação e rotação (c). As vigas apoiadas por diversos apoios intermediários são chamadas vigas contínuas (d). Se as duas extremidades são fixas pelos apoios, é denominada viga engastada (e). Neste conteúdo, discutiremos apenas as vigas determinadas, que podem ser analisadas pelas três equações da estática.

Os pórticos são elementos estruturais compostos de vigas e colunas conectadas por ligações rígidas. O ângulo entre a viga e a coluna normalmente é de 90°. Como mostrado em a e b, os pórticos podem consistir em uma única coluna e viga ou, como em um prédio de vários andares, de muitas colunas e vigas.

O arco utiliza material de modo eficiente, pois as cargas aplicadas criam principalmente compressão axial sobre todas as seções transversais. Os arcos são classificados pelo número de articulações que contêm ou pela maneira com que suas bases são construídas. Os arcos são classificados pelo número de articulações que contêm ou pela maneira com que suas bases são construídas. A Figura mostra os três tipos principais: triarticulado, biarticulado e de extremidades fixas. O arco triarticulado é estaticamente determinado; os outros dois tipos são indeterminados. O arco triarticulado é o mais fácil de analisar e construir.

Aula Concluída!
Avançar