Segundo Sussekind, vol.1 1989, pg. 276:
um sistema de forças paralelas no espaço é regido por três equações da estática, sendo duas de momentos nulos em relação a dois eixos situados num plano perpendicular ao das forças e a terceira da soma das projeções de todas as forças igual a zero, segundo um eixo paralelo.
(SUSSEKIND, 1989, vol. 1, pg. 276)

Define-se então grelha como sendo uma estrutura plana submetida a carregamento perpendicular a seu plano. Considerado as equações da estática:
\[ \sum Z=0 \\ \sum {{M}_{x}}=0 \\ \sum {{M}_{y}}=0\]

Uma grelha será isostática quando tivermos apenas três incógnitas a determinar. A primeira imagem mostra uma grelha engastada-livre e no segundo uma grelha triapoiada.
Observando o funcionamento de uma grelha podemos afirmar que suas barras, em uma seção genérica qualquer, podem estar sujeitas a três esforços simples: Esforço Cortante (Q), Momento Fletor (M) e Momento Torsor (Mt), que devem ser calculados e expressos sob a forma de um diagrama. Podemos adotara a seguinte convenção de sinais:
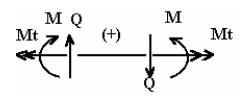
Conhecendo as reações de apoio, pode-se determinar os esforços solicitantes numa seção genérica S da grelha. Podemos afirmar que numa seção genérica de uma grelha, podem atuar três esforços simples: um esforço cortante Q, perpendicular ao plano da grelha, um momento fletor M, produzindo flexão num plano perpendicular ao da grelha e um momento torsor T.
A resolução de uma estrutura plana submetida a um carregamento mais geral, oblíquo ou plano, se fará decompondo o carregamento oblíquo em componentes perpendiculares ao plano e em componentes pertencentes ao plano. Para se obter os diagramas solicitantes numa estrutura plana submetida a um carregamento qualquer, resolvemos separadamente os dois casos em que este carregamento se decompões (grelha e estrutura plana) e os diagramas solicitantes de cada um destes dois casos de carregamentos são finais.
(SUSSEKIND, 1989, vol.1, pg. 279)

Portanto para se obter os diagramas solicitantes para a grelha, cujas barras formam em todos os nós ângulos retos, devemos analisar, por exemplo, pelo método direto, cada barra, levando-se em consideração os seus pontos de transição e em cada nó fazermos a conversão das solicitações devido a mudança de direção.
O momento fletor que atua em uma determinada barra, fará o efeito de torsor em uma barra perpendicular a citada e vice-versa.
Observemos o exemplo abaixo de uma grelha engastada:

Em uma grelha engastada e livre, não é necessário o cálculo prévio das reações vinculares, pois os diagramas solicitantes podem ser obtidos à partir da parte livre (Balanço) até o engaste.
Fazemos sempre o estudo barra por barra, iniciando-se, no caso pela barra AB que funcionará como uma viga engastada em B e livre em A. Os demais passos serão como nos demais casos, percorrendo a estrutura toda, passando por todas as barras.

A partir dos esquemas vistos podemos obter facilmente os diagramas dos esforços solicitantes para a grelha.

Observemos o exemplo abaixo de uma grelha tri apoiada:

\[ \sum {{M}_{BC}}=0\text{ }\!\!~\!\!\text{ }\to 10\text{ }\!\!~\!\!\text{ }x\text{ }\!\!~\!\!\text{ }4+30\text{ }\!\!~\!\!\text{ }x\text{ }\!\!~\!\!\text{ }4+40\text{ }\!\!~\!\!\text{ }x\text{ }\!\!~\!\!\text{ }2-4\text{ }\!\!~\!\!\text{ }{{V}_{E}}=0\text{ }\!\!~\!\!\text{ }\to \text{ }\!\!~\!\!\text{ }{{V}_{E}}=60\text{ }\!\!~\!\!\text{ }kN \\ \sum {{M}_{CE}}=0\text{ }\!\!~\!\!\text{ }\to 30\text{ }\!\!~\!\!\text{ }x\text{ }\!\!~\!\!\text{ }2-10\text{ }\!\!~\!\!\text{ }x\text{ }\!\!~\!\!\text{ }2-40x\text{ }\!\!~\!\!\text{ }2+2\text{ }\!\!~\!\!\text{ }{{V}_{B}}=0\text{ }\!\!~\!\!\text{ }\to \text{ }\!\!~\!\!\text{ }{{V}_{E}}=20\text{ }\!\!~\!\!\text{ }kN \\ \sum {{F}_{v}}=0\text{ }\!\!~\!\!\text{ }\to \text{ }\!\!~\!\!\text{ }{{V}_{C}}+{{V}_{B}}+{{V}_{E}}-40-10-30\text{ }\!\!~\!\!\text{ }=0\text{ }\!\!~\!\!\text{ }\to \text{ }\!\!~\!\!\text{ }{{V}_{c}}=0\text{ }\!\!~\!\!\text{ }kN\]

Até o momento analisamos estruturas considerando carregamentos sem considerar a posição e não fizemos distinção entre a carga permanente, que tem posição ixs, e sobrecarga, que pode mudar de posição. Para tanto devemos conhecer os conceitos de cargas móveis (por exemplo, um caminhão ou um trem) para maximizar o valor de certo tipo de força (cortante ou momento em uma viga ou axial em uma treliça) em uma seção designada de uma estrutura.
(LEET; UANG; GILBERT, 2010, pag. 275)
À medida que uma carga em movimento passa por uma estrutura, as forças internas em cada ponto da estrutura variam.
Intuitivamente, reconhecemos que uma carga concentrada aplicada em uma viga em meio vão produz tensões de flexão e deflexão muito maiores do que a mesma carga aplicada perto de um apoio.
Se uma estrutura deve ser projetada com segurança, devemos dimensionar suas barras e nós de modo que a força máxima em cada seção, produzida pela sobrecarga e pela carga permanente, seja menor ou igual à capacidade admissível da seção. Para estabelecer as forças de projeto máximas nas seções críticas, produzidas por cargas que se movem, frequentemente construímos linhas de influência.
Linha de influência é um diagrama cujas ordenadas, que são plotadas como uma função da distância ao longo do vão, e fornecem o valor de uma força interna, uma reação ou um deslocamento em um ponto específico de uma estrutura quando uma carga unitária de 1 kip ou 1 kN se move pela estrutura.
Uma vez construída a linha de influência, podemos utilizá-la (1) para determinar onde devemos colocar carga móvel em uma estrutura para maximizar a força (cortante, momento etc.) para a qual a linha de influência é desenhada e (2) para avaliar a magnitude da força (representada pela linha de influência) produzida pela carga móvel. Embora represente a ação de uma única carga em movimento, a linha de influência também pode ser usada para estabelecer a força em um ponto produzida por várias cargas concentradas ou por uma carga uniformemente distribuída
(LEET; UANG; GILBERT, 2010, pag. 276)
Para construir uma linha de influência usaremos o exemplo da viga da fira na qual desenharemos a linha de influência da reação RARA no apoio A com apoio simples(a).

Conforme observado anteriormente, podemos estabelecer as ordenadas das linhas de influência para a reação em A calculando o valor de RARA para sucessivas posições de uma carga unitária à medida que ela se move pelo vão. Começamos colocando a carga unitária no apoio A. Somando os momentos sobre o apoio B (b), calculamos RARA= 1 kip.

Então, movemos a carga unitária arbitrariamente para uma segunda posição, localizada a uma distância L/4 à direita do apoio A. Novamente, somando os momentos sobre B, calculamos RA= 34 kipsRA= 34 kips (c). Em seguida, movemos a carga para o meio vão e calculamos RA= 12 kipsRA= 12 kips (d).

Para o cálculo final, posicionamos a carga de 1 kip diretamente sobre o apoio B e calculamos R_A= 0 (e). Para construir a linha de influência, plotamos agora os valores numéricos de R_A diretamente abaixo de cada posição da carga unitária associada ao valor de RA correspondente. O diagrama de linha de influência resultante está mostrado em (f).
(LEET; UANG; GILBERT, 2010, pag. 258)

A linha de influência mostra que a reação em A varia linearmente de 1 kip, quando a carga está em A, até o valor 0, quando a carga está em B. Como a reação em A é avaliada em kips, as ordenadas da linha de influência têm unidades de kips por 1 kip de carga. Quando você se familiarizar com a construção de linhas de influência, precisará colocar a carga unitária em apenas duas ou três posições ao longo do eixo da viga para estabelecer o formato correto da linha de influência. Abaixo os passos para traçar a linha de influência:
Plotando os valores da reação de B para várias posições da carga unitária, geramos a linha de influência de R_B mostrada em (g). Como a soma das reações em A e B sempre deve ser igual a 1 (o valor da carga aplicada) para todas as posições da carga unitária, a soma das ordenadas das duas linhas de influência em qualquer seção também deve ser igual a 1 kip.
(LEET; UANG; GILBERT, 2010, pag. 259)

Conforme observado anteriormente, construímos linhas de influência para estabelecer o valor máximo das reações ou das forças internas produzidas por carga móvel. Podemos descrever uma linha de influência para calcular o valor máximo de uma função, quando a carga móvel, que pode atuar em qualquer parte da estrutura, é uma única carga concentrada ou uma carga uniformemente distribuída de comprimento variável. Como a ordenada de uma linha de influência representa o valor de determinada função produzido por uma carga unitária, o valor produzido por uma carga concentrada pode ser estabelecido multiplicando a ordenada da linha de influência pela magnitude da carga concentrada.
Esse cálculo simplesmente reconhece que as forças criadas em uma estrutura elástica são diretamente proporcionais à magnitude da carga aplicada.
Se a linha de influência é positiva em algumas regiões e negativa em outras, a função representada por ela inverte de direção para certas posições da carga móvel.
Para projetar membros nos quais a direção da força tem influência significativa no comportamento, devemos estabelecer o valor da força máxima em cada direção, multiplicando as ordenadas máximas positivas e máximas negativas da linha de influência pela magnitude da carga concentrada. Por exemplo, se uma reação de apoio inverte de direção, o apoio deve ser detalhado para transmitir os valores máximos de tração (elevação), assim como o valor máximo de compressão na fundação.
No projeto de prédios e pontes, a carga móvel é frequentemente representada por uma carga uniformemente distribuída. Por exemplo, um código de construção pode exigir que os pisos dos estacionamentos sejam projetados para uma carga móvel uniformemente distribuí da de certa magnitude, em vez de um conjunto especificado de cargas de roda.
(LEET; UANG; GILBERT, 2010, pag. 280)
Construir a linha de influência das reações A da viga:

Para estabelecer uma expressão geral para os valores de RARA para qualquer posição da carga unitária entre os apoios A , colocamos a carga unitária a uma distância x1 à direita do apoio A

\[ \sum {{M}_{C}}=0\text{ }\!\!~\!\!\text{ }\to 10\text{ }\!\!~\!\!\text{ }{{R}_{A}}-\left( 1 \right)(10-\text{ }\!\!~\!\!\text{ }{{x}_{1}})=0 \\ {{R}_{A}}=1-\text{ }\!\!~\!\!\text{ }\frac{{{x}_{1}}}{10\text{ }\!\!~\!\!\text{ }}\text{ }\!\!~\!\!\text{ }em\text{ }\!\!~\!\!\text{ }que\text{ }\!\!~\!\!\text{ }0\text{ }\!\!~\!\!\text{ }\le {{x}_{1}}\le 10\]
Avaliando \({{R}_{A}}\) teremos:

Podemos traçar então a linha de influência do apoio A:

Aula Concluída!
Inicio