Treliça é um elemento estrutural composto de um arranjo estável de barras delgadas interligadas O padrão das barras, que frequentemente subdivide a treliça em áreas triangulares, é selecionado para produzir um membro de apoio leve e eficiente.
Conclui-se desta forma que as barras da treliça transmitem somente força axial- tração ou compressão. Como as barras da treliça atuam em tensão direta, eles transmitem carga eficientemente e em geral têm seções transversais relativamente pequenas.

Geralmente, o custo por quilograma da fabricação de uma treliça é maior do que o custo para laminar uma viga de aço; entretanto, a treliça exigirá menos material, pois ele é utilizado mais eficientemente. Em uma estrutura de vão longo, digamos 60 metros ou mais, o peso pode representar a maior parte (na ordem de 75% a 85%) da carga de projeto a ser suportada. Usando treliça, em vez de viga, o engenheiro muitas vezes pode projetar uma estrutura mais leve e mais resistente, a um custo reduzido. Além de variar a área das barras da treliça, o projetista pode modificar a profundidade da treliça para reduzir seu peso.
(LEET, KENNETH M., pag. 124)
As diagonais de uma treliça normalmente se inclinam para cima em um ângulo que varia de 45° a 60°. Se uma treliça suporta cargas iguais ou praticamente iguais em todos os nós, a direção na qual as diagonais se inclinam determinará se elas transmitem forças de tração ou compressão.

Considerando que as treliças a carregamentos apenas nos nós com extremidades rotuladas não teremos atuação de esforços de momento e cortantes, apenas existindo esforços normais. Sendo assim as grandezas a determinar para sua resolução, as reações de apoio, como por exemplo da figura abaixo, HA, VA e VB.

Um método para estabelecer uma treliça estável é construir uma unidade triangular básica e então fixar nós adicionais, estendendo barras a partir dos nós do primeiro elemento triangular. As treliças formadas dessa maneira são chamadas treliças simples.
Se duas ou mais treliças simples são conectadas por um pino ou por um pino e um tirante, a treliça resultante é denominada treliça composta. Por fim, uma treliça — normalmente com formato incomum — que não é simples nem composta é denominada treliça complexa

A análise utilizada para avaliar as forças das barras é baseada nas três suposições a seguir:
Estabelecemos uma força de tração como positiva e uma força de compressão como negativa.
Alternativamente, podemos estipular o caráter de uma força adicionando um T após seu valor numérico para indicar força de tração ou um C para indicar força de compressão. Se a barra está em tração, as forças axiais nas suas extremidades atuam para fora e tendem a alongar a barra. Transmissão de cargas para treliças e mostrado abaixo ( Sussekind, volume1):

As forças iguais e opostas nas extremidades da barra representam a ação dos nós na barra.
Como a barra aplica forças iguais e opostas nos nós, uma barra em tração aplicará uma força que atua para fora, a partir do centro do nó. Se a barra está em compressão, as forças axiais nas suas extremidades atuam para dentro e comprimem a barra. Uma barra em compressão faz pressão contra o nó (isto é, aplica uma força dirigida para dentro, em direção ao centro do nó).
Condições para obtenção de uma treliça isostática:
O número de incógnitas é dados por:
Desta forma, podemos classificá-las da seguinte maneira:
Abaixo apresentamos alguns exemplos de treliças aplicado a outros Sistemas estruturais:




Para determinar as forças das barras pelo método dos nós, analisamos os diagramas de corpo livre dos nós. O diagrama de corpo livre é estabelecido supondo-se que seccionamos as barras por uma seção imaginária exatamente antes do nó.
Por exemplo, para determinaras forças das barras nos membros AB e BC, usamos o corpo livre do nó B, mostrado na Figura. Como as barras transmitem força axial, a linha de ação de cada força de barra é dirigida ao longo do eixo longitudinal da barra.
Como todas as forças que atuam em um nó passam pelo pino, elas constituem um sistema de forças concorrentes. Para esse tipo de sistema de forças, estão disponíveis somente duas equações da estática (ou seja, \(\sum f x = 0\) e \(\sum f y = 0\) para avaliar forças de barra desconhecidas. Como somente duas equações de equilíbrio estão disponíveis, só podemos analisar nós que contêm no máximo duas forças de barra desconhecidas.
O analista pode seguir diversos procedimentos no método dos nós.
Se somente uma força desconhecida atua em uma direção específica, os cálculos são efetuados mais rapidamente somando-se as forças nessa direção. Após uma componente ser calculada, a outra componente pode ser encontrada pela definição de uma proporção entre as componentes da força e a inclinação da barra (obviamente, as inclinações da barra e da força da barra são idênticas). Se a solução de uma equação de equilíbrio produz um valor de força positivo, a direção suposta inicialmente para a força estava correta. Por outro lado, se o valor da força é negativo, sua magnitude está correta, mas a direção suposta inicialmente estava incorreta e deve ser invertida no esboço do diagrama de corpo livre.
Após as forças de barra serem estabelecidas em um nó, o engenheiro passa para os nós adjacentes e repete o cálculo anterior, até que todas as forças de barra sejam avaliadas (Leet, Kenneth M., pag. 129).

Isolando os nós (B) para calcular as forças:

Abaixo faça uma análise da treliça considerando as reações conhecidas:


Para iniciar a análise, devemos começar em um nó com no máximo duas barras. Os nós A ou C são aceitáveis. Como os cálculos são mais simples em um n com uma única barra inclinada, começamos em A. Sobre um corpo livre do nó A (ver Figura b), supomos arbitrariamente que as forças de barra FAB e FAD são forças de tração e as mostramos atuando para fora no nó. Em seguida, substituímos FAB por suas componentes retangulares XAB e YAB. Escrevendo a equação de equilíbrio na direção y, calculamos YAB.
\[\sum fy 0 \\ 0 = -24 + Y_{AB} \\ Y_{AB} = 24kips\]
Como YAB é positiva, trata-se de uma força de tração, e a direção suposta no esboço estava correta. Calcule XAB e FAB pela proporção, considerando a inclinação da barra
Considerando a treliça abaixo calculamos as reações e esforços pelo equilíbrio dos nós:

\[\sum f_{x}=0 \rightarrow3- R_{AX} =0 \rightarrow R_{AX} =3 tf \\ \sum M_{A}=0 \rightarrow3 R_{By} - 6\times1,5-3 \times 2 =0 \rightarrow R_{By}=t_{f} \\ \sum F_{y}=0 \rightarrow R_{Ay} +5-6=0 \rightarrow R_{Ay}= 1 tf\]
NÓ A:
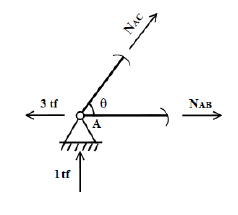
\[ \sum F_{y}=0 \rightarrow + 1 N_{AC} \times SEN 53,13 = 0 \rightarrow N_{AC}= - 1,25TF tf\]
NÓ B:

\[ \sum {{F}_{y}}=0\text{}\!\!~\!\!\text{ }\to 5+{{N}_{BC}}X\text{ }\!\!~\!\!\text{ }SEN\text{}\!\!~\!\!\text{ }53,13=\text{ }\!\!~\!\!\text{ }0\text{ }\!\!~\!\!\text{ }\!\!~\!\!\text{ }\to \text{ }\!\!~\!\!\text{}{{N}_{AC}}=-6,25TF\text{ }\!\!~\!\!\text{ }tf\]
Aula Concluída!
Avançar