Para analisar uma treliça estável pelo método das seções, consideramos que a treliça é dividida em dois corpos livres, passando um plano de corte imaginário pela estrutura.
O plano de corte deve, evidentemente, passar pela barra cuja força deve ser determinada. Em cada ponto onde uma barra é cortada, a força interna da barra é aplicada na face do corte como uma carga externa. Embora não haja nenhuma restrição para o número de barras que podem ser cortadas, frequentemente utilizamos seções que cortam três barras, pois estão disponíveis três equações de equilíbrio estático para analisar um corpo livre. Por exemplo, se quisermos determinar as forças de barra nas cordas e na diagonal de um painel interno da treliça da Figura a, podemos passar uma seção vertical pela treliça, produzindo o diagrama de corpo livre mostrado na Figura b.
Como vimos no método dos nós, o engenheiro está livre para pressupor a direção da força na barra. Se uma força for presumida na direção correta, a solução da equação de equilíbrio produzirá um valor de força positivo. Alternativamente, um valor de força negativo indica que a direção da força foi suposta incorretamente.
Vamos analisar a treliça usando o método das seções e calcular as forças nas barras HC, HG, e BC da treliça.

Passando a seção 1-1 pela treliça, cortando o corpo livre mostrado na Figura b. A direção da força axial em cada barra é pressuposta arbitrariamente. Para simplificar os cálculos, a força FHC é decomposta nas componentes vertical e horizontal. Calculando YHC.</p>
\[ \sum {{F}_{y}}=0\text{ }\!\!~\!\!\text{ }\to 50-40-{{Y}_{HC}}=0\text{}\!\!~\!\!\text{ }\!\!~\!\!\text{ }\to \text{ }\!\!~\!\!\text{ }{{Y}_{HC}}=10\text{ }\!\!~\!\!\text{ }Kips\]
Da relação da inclinação:
\[ \frac{{{X}_{HC}}}{3}=\text{}\!\!~\!\!\text{ }\frac{{{Y}_{HC}}}{4} \\ {{X}_{HC}}=\text{}\!\!~\!\!\text{ }\frac{3}{4}{{Y}_{HC}}=7,5,\text{ }\!\!~\!\!\text{ }Kips\]
Calcule FBC. Some os momentos sobre um eixo através de H na intersecção das forças FHG e FHC:
\[ \sum {{M}_{H}}=0\text{ }\!\!~\!\!\text{ }\to 30\text{ }\!\!~\!\!\text{ }\left( 20 \right)+50\text{ }\!\!~\!\!\text{ }\left( 15 \right)-\text{ }\!\!~\!\!\text{ }{{F}_{BC}}\left( 20 \right)=0\text{ }\!\!~\!\!\text{ }\!\!~\!\!\text{ }\to \text{ }\!\!~\!\!\text{ }{{F}_{BC}}=67,5\text{ }\!\!~\!\!\text{ }Kips \\ \sum {{F}_{x}}=0\text{ }\!\!~\!\!\text{ }\to 30-{{F}_{HG}}+{{X}_{HC}}+\text{ }\!\!~\!\!\text{ }{{F}_{BC}}-30=0\text{ }\!\!~\!\!\text{ }\!\!~\!\!\text{ }\to \text{ }\!\!~\!\!\text{ }{{F}_{HG}}=75\text{ }\!\!~\!\!\text{ }Kips\]
Como a solução das equações de equilíbrio acima produziu valores de força positivos, as direções das forças mostradas na Figura b estão corretas.
A ideia do método das seções seria, portando determinar esforços axiais partindo a estrutura em partes, considerando um dos lados e colocando esforços internos que surgem nas barras para estabelecer o equilíbrio.


As forças N3, N6 e N10 representam a ação da parte da direita da treliça sobre a parte da esquerda. Os esforços indicados N3, N6 e N10 são iguais em módulo e direção, mas têm os sentidos opostos dos que aparecem na parte esquerda. Representam a ação da parte esquerda sobre a parte da direita. Para obter os esforços N3, N6 e N10 utilizam-se as equações da estática, devendo ser escolhidas e usadas numa ordem tal que permita determinar cada incógnita diretamente.
\[ \sum{{M}_{c}}=0\text{ }\!\!~\!\!\text{ }obtem-se\text{ }\!\!~\!\!\text{ }N3 \\ \sum {{M}_{D}}=0\text{ }\!\!~\!\!\text{ }obtem-se\text{ }\!\!~\!\!\text{ }N6 \\ \sum {{F}_{y}}=0\text{ }\!\!~\!\!\text{ }obtem-se\text{ }\!\!~\!\!\text{ }N10\]
Se os esforços forem positivos terão o sentido indicado (tração) senão terão sentido inverso (compressão).
As seções apresentadas anteriormente nesta unidade abordaram a análise de treliças baseada nas suposições de que (1) as barras são conectadas aos nós por meio de pinos sem atrito e (2) as cargas são aplicadas apenas nos nós. Nos casos em que as cargas de projeto são escolhidas de forma conservadora e as deflexões não são excessivas, com o passar dos anos essas suposições simplificadas geralmente têm produzido projetos satisfatórios.
É por isso que, no passado, a análise de treliças era simplificada, permitindo aos projetistas pressupor nós ligados por pinos. Agora que existem programas de computador, podemos analisar treliças determinadas e indeterminadas como uma estrutura de nós rígidos para propiciar uma análise mais precisa, sendo que a limitação de que as cargas precisam ser aplicadas nos nós não é mais uma restrição. Como os programas de computador exigem valores de propriedades da seção transversal das barras — área e momento de inércia —, as barras devem ser dimensionadas inicialmente.
O arco utiliza material de modo eficiente, pois as cargas aplicadas criam principalmente compressão axial sobre todas as seções transversais. Neste capítulo, mostraremos que, para um conjunto de cargas em particular, o projetista pode estabelecer um formato de arco — a forma funicular — no qual todas as seções estão em compressão direta (os momentos são zero).
Normalmente, o peso próprio constitui a principal carga suportada pelo arco. Se uma forma funicular basear-se na distribuição do peso próprio, serão criados momentos nas seções transversais pelas sobrecargas, cuja distribuição difere daquela do peso próprio. Mas, normalmente, na maioria dos arcos, as tensões de flexão produzidas pelos momentos da sobrecarga são tão pequenas comparadas às compressões axiais, que existem tensões de compressão líquidas em todas as seções.
Como os arcos usam material com eficiência, os projetistas frequentemente os empregam como os principais elementos estruturais em pontes de vão longo (digamos, de 120 m a 550 m, aproximadamente) ou em edificações que exigem grandes áreas livres de colunas; por exemplo, hangares de avião, ginásios esportivos ou salas de conferências.</p>
(LEET, KENNETH M., pag. 241)
Se considerarmos um cabo AB submetido a cargas concentradas disposto da seguinte forma:

Se rebatermos o cabo AB e mantendo sua forma funicular “congelada” de maneira que o cabo possua rigidez suficiente para resistir a esforços de compressão, o cabo se transforma num arco poligonal funicular, onde todas seções transversais estão submetidas exclusivamente à esforços de compressão.
Nos cabos, para cada tipo e intensidade de carregamento a forma funicular seria diferente de forma que todas seções transversais estivessem submetidas a momentos nulos. Nos arcos, para cada tipo e intensidade de carregamento existirá uma forma funicular para a qual os momentos serão nulos para todas as seções transversais.
Esta forma funicular é chamada “linha de pressão” de um carregamento sempre que a geometria de um arco coincidir com a linha de pressão do carregamento aplicado sobre o arco os únicos esforços atuantes serão de compressão.
Abaixo apresentamos algumas formas funiculares para alguns tipos de carregamentos:

Porém, o comportamento dos arcos difere do comportamento dos cabos em um aspecto básico: se o carregamento no cabo se modifica, o cabo muda de forma e assume uma nova geometria funicular. Por outro lado, se o carregamento no arco se altera, o arco mantém sua geometria, devido a sua maior rigidez ao compará-lo ao cabo, e não possui mais uma forma funicular para a nova condição de carregamento.

A geometria triangular não coincide com a linha de pressão para 2 cargas concentradas. Quando a geometria do arco não
coincide com a linha de pressão para o carregamento, surgem esforços de flexão e cisalhamento no arco (Ms,Vs), além dos esforços de compressão (Ns).
Ao projetar-se a forma de um arco, sob o ponto de vista estrutural, deve ser escolhida a forma funicular para o carregamento aplicado. No entanto, sabe-se que as estruturas estão submetidas a carregamentos permanentes (peso próprio) e a carregamentos variáveis (pessoas, mobiliário, ventos). Para qual combinação de carregamentos definiremos a geometria do arco? Se definirmos somente em função do carregamento permanente haverá efeitos de flexão quando aplicado o carregamento variável. Se a geometria do arco for definida com o conjunto de carga permanente + variável, para qualquer alteração no carregamento variável ocorrerão efeitos de flexão e cisalhamento.
Os romanos notabilizaram-se pela utilização de arcos para vencer grandes vãos. Os arcos romanos possuem a forma de um semicírculo.
O carregamento que possui o semicírculo como a linha de pressão é a ação de cargas radiais. Esse tipo de carregamento surge quando há efeitos de vento envolvendo uma. cobertura com estrutura em arco, por exemplo. Na maioria dos casos, o carregamento será do tipo uniformemente distribuído, o que ocasiona surgimento de efeitos de flexão nos arcos romanos. É o predomínio da forma sobre a função estrutural.

Outro tipo de arco bastante utilizado no passado é o arco gótico, que possui uma flecha bastante pronunciada. Lembrando-se do elenco de cabos, quanto maior a flecha, menos a reação horizontal (empuxo) nos apoios. Nos arcos vale a mesma reação. Os arcos góticos possuem a vantagem de minimizarem as reações horizontais, permitindo vencer grandes vãos sem a preocupação de surgirem altos empuxos.

Os arcos góticos possuem a vantagem de minimizarem as reações horizontais, permitindo vencer grandes vãos sem a preocupação de surgirem altos empuxos.
Além da escolha da geometria do arco, é necessário que também seja garantido que o empuxo horizontal nos apoios seja absorvido pela fundação.
No caso de pontes, os sistemas em arco podem apresentar duas configurações diferentes, conforme a posição relativa do tabuleiro da ponte esteja acima ou abaixo do arco.
Quanto à vinculação, os arcos podem apresentar extremidades rotuladas ou engastadas:

Os arcos com apoios rotulados permitem a rotação nas extremidades quando o carregamento atuar.
Os arcos com vínculos engastados são mais rígidos que os de extremidade rotulada, apresentando menores deslocamentos quando sob a ação do carregamento. Por serem mais rígidos, adaptam-se menos às variações de carregamento ao longo da vida da estrutura, surgindo assim esforços solicitantes mais elevados que nos pórticos rotulados.
Exemplos de arcos aplicados na engenharia:

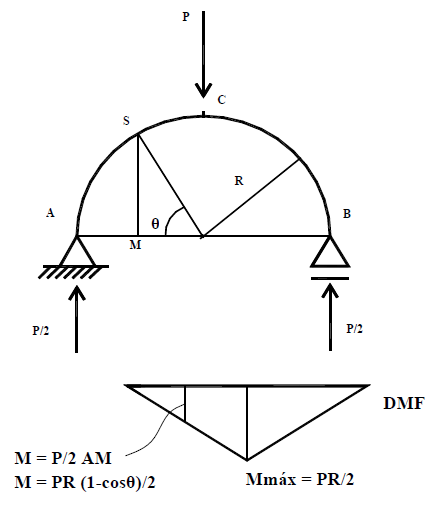
Exemplo: Calcular as reações do arco abaixo:

\[ {{Q}_{s}}=\text{ }\!\!~\!\!\text{ }{{V}_{A}}\text{ }\!\!~\!\!\text{ }\sin \theta =\text{ }\!\!~\!\!\text{ }\frac{P\text{ }\!\!~\!\!\text{ }\sin \theta }{2}\text{ }\!\!~\!\!\text{ } \\ {{N}_{s}}=\text{ }\!\!~\!\!\text{ }-{{V}_{A}}\text{ }\!\!~\!\!\text{ }\cos \theta =-\text{ }\!\!~\!\!\text{ }\frac{P\text{ }\!\!~\!\!\text{ }\cos \theta }{2}\text{ }\!\!~\!\!\text{ } \\ {{M}_{s}}=\text{ }\!\!~\!\!\text{ }{{V}_{A}}(\text{ }\!\!~\!\!\text{ }R-R\text{ }\!\!~\!\!\text{ }\cos \theta =\text{ }\!\!~\!\!\text{ }\frac{P\text{ }\!\!~\!\!\text{ }R\text{ }\!\!~\!\!\text{ }(1-\cos \theta )}{2}\text{ }\!\!~\!\!\text{ }\]
Aula Concluída!
Avançar