Segundo Leet, Uang e Gilbert (2010, pag. 169):
as vigas representam um dos elementos mais comuns encontrados em estruturas. Quando uma viga é carregada perpendicularmente ao seu eixo longitudinal, forças internas — cortante e momento — desenvolvem-se para transmitir as cargas aplicadas para os apoios. Se as extremidades da viga são restritas longitudinalmente por seus apoios ou se a viga é componente de um pórtico contínuo, uma força axial também pode se desenvolver.
(LEET; UANG; GILBERT, 2010, pag. 169)
Para projetar uma viga, o engenheiro deve construir os diagramas de cortante e momento para determinar o local e a magnitude dos valores máximos dessas solicitações.
A não ser para vigas curtas e pesadamente carregadas, cujas dimensões são controladas pelos requisitos de cortante, as proporções da seção transversal são determinadas pela magnitude do momento máximo no vão.
Por fim, as deflexões produzidas pelas cargas de serviço devem ser verificadas para garantir que a peça tenha rigidez adequada.
Os limites da deflexão são definidos pelos códigos estruturais.
A última etapa no projeto de uma viga é verificar se ela não deforma excessivamente (isto é, se as deflexões estão dentro dos limites especificados pelo código de projeto aplicável). As vigas excessivamente flexíveis sofrem grandes deflexões que podem danificar a construção não estrutural associada: tetos de gesso, paredes de alvenaria e tubulações rígidas, por exemplo, podem rachar.
Normalmente, as vigas são classificadas pela maneira com que são apoiadas. Uma viga apoiada por uma articulação fixa em uma extremidade e por uma articulação móvel na outra extremidade é chamada viga com apoio simples (a), se a extremidade com apoio simples se estende sobre um apoio, denomina-se viga em balanço (b), uma viga em balanço é fixa em uma extremidade, contra translação e rotação (c), As vigas apoiadas por diversos apoios intermediários são chamadas vigas contínuas (d).

Conforme o estudo das vigas nos cursos de mecânica dos materiais e estática, cortante e momento são as forças internas em uma viga ou pórtico, produzidas pelas cargas transversais aplicadas.
O cortante atua perpendicularmente ao eixo longitudinal, e o momento representa o conjugado interno produzido pelas tensões de flexão.

A figura mostra a convenções de sinal para cortante e momento, no qual (a) representa a viga cortada pela seção 1, o (b) o cortante V e o momento M ocorrem como pares de forças internas, o (c) cortante positivo: a resultante R das forças externas no corpo livre à esquerda da seção atua para cima; (d) momento positivo; (e) momento negativo.
Nas vigas, força cortante e momento fletor normalmente variam de acordo com a distância, x, da posição da seção transversal em que ocorrem. Quando se projeta uma viga, é desejável que se conheçam os valores de V e M em todas as seções transversais e um modo adequado de obter essa informação é por meio de um gráfico que mostre a variação desses valores ao longo do eixo da viga. Para traçar esse gráfico, toma-se a posição da seção transversal como abscissa e os valores correspondentes da força cortante e do momento fletor como ordenadas. Tais gráficos são chamados diagramas de forças cortantes e de momentos fletores. Observe a viga abaixo:

Considere-se uma viga simplesmente apoiada, AB, com uma carga concentrada P (acima). As reações dos apoios são:
\[ {{R}_{A}}=\text{}\!\!~\!\!\text{ }\frac{P\text{ }\!\!~\!\!\text{ }b}{L}\text{ }\!\!~\!\!\text{}e\text{ }\!\!~\!\!\text{ }{{R}_{B}}=\text{ }\!\!~\!\!\text{ }\frac{P\text{}\!\!~\!\!\text{ }a}{L}\]
Estas reações representam os esforços cortantes que atuam na viga sendo portanto:
\[ V=\frac{Pb}{L}\text{ e o momento na seção distante} \times \text{do apoio A seria M} = \frac{P_{a}}{L} x\]
Estas expressões mostram que a força cortante permanece constante do apoio A até o ponto de aplicação da carga, enquanto o momento fletor é função linear de x. Para x = 0, o momento é nulo; para x=a, é igual a Pab/L. Os diagramas correspondentes a essa parte, para a força cortante e para o momento fletor, seria:

Portanto, para projetar uma viga, devemos estabelecer a magnitude do cortante e do momento (e da carga axial, se for significativa) em todas as seções ao longo do eixo da barra. Se a seção transversal de uma viga é constante ao longo de seu comprimento, é projetada para os valores máximos de momento e cortante dentro do vão. Se a seção transversal varia, o projetista deve investigar mais seções para verificar se a capacidade da barra é adequada para suportar o cortante e o momento.
Para fornecer essas informações graficamente, construímos diagramas de cortante e de momento. Essas curvas, que de preferência devem ser desenhadas em escala, consistem em valores de cortante e momento plotados como ordenadas em relação à distância ao longo do eixo da viga. Embora possamos construir curvas de cortante e de momento cortando corpos livres em intervalos ao longo do eixo de uma viga e escrever equações de equilíbrio para estabelecer os valores de cortante e momento em seções específicas, é muito mais simples construir essas curvas a partir das relações básicas existentes entre carga, cortante e momento
(LEET; UANG; GILBERT, 2010, pag. 180)
Considere-se, agora, o caso de uma viga simplesmente apoiada, com uma carga uniformemente distribuída. As reações RARA e RARA são iguais a qL/2. Numa seção transversal, à distância x da extremidade esquerda A:
\[V=q\text{ }\!\!~\!\!\text{ }\frac{L}{2}-qx \text{ e } M=q\text{ }\!\!~\!\!\text{ }\frac{L}{2}-q\frac{{{x}^{2}}}{2}\]
Da primeira dessas equações, vê-se que o diagrama de forças cortantes consiste numa linha reta inclinada que tem nos pontos x = 0 e x = L as ordenadas qL/2 e - qL/2, respectivamente. O diagrama de momentos fletores é uma parábola, simétrica em relação ao meio da viga. Os momentos fletores nas extremidades são nulos e o valor máximo ocorre no meio do vão, onde o diagrama de forças cortantes muda de sinal. Esse máximo é calculado fazendo x = L/2 na expressão (j), o que fornece o valor de:
\[ {{M}_{m\text{ }\!\!\acute{\mathrm{a}}\!\!\text{ }x}}=\text{ }\!\!~\!\!\text{ }\frac{q{{l}^{2}}}{8}\]

Tracemos o diagrama das vigas das figuras:
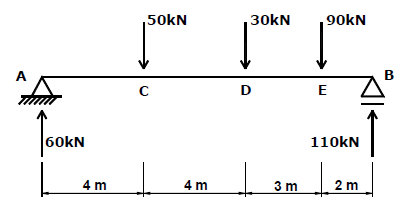
Calculando os momentos nas seções teremos:
\[ M_{C}^{ESQ}=60\text{ }\!\!~\!\!\text{ }X\text{ }\!\!~\!\!\text{}4=240\text{ }\!\!~\!\!\text{ }kN \\ M_{D}^{ESQ}=60\text{ }\!\!~\!\!\text{ }X\text{ }\!\!~\!\!\text{ }8-50\text{}\!\!~\!\!\text{ }X\text{ }\!\!~\!\!\text{ }4\text{ }\!\!~\!\!\text{}=280\text{ }\!\!~\!\!\text{ }kN \\ M_{D}^{DIR}=110\text{ }\!\!~\!\!\text{ }X\text{ }\!\!~\!\!\text{ }2\text{}\!\!~\!\!\text{ }=220\text{ }\!\!~\!\!\text{ }kN \\ M_{E}^{ESQ}=60\text{ }\!\!~\!\!\text{ }X\text{ }\!\!~\!\!\text{ }11-50\text{ }\!\!~\!\!\text{ }X\text{ }\!\!~\!\!\text{ }7\text{ }\!\!~\!\!\text{ }-30\text{ }\!\!~\!\!\text{ }X\text{ }\!\!~\!\!\text{ }3=220\text{ }\!\!~\!\!\text{ }kN\]
Traçamos os diagramas


Calculando os momentos nas seções teremos:
\[ M_{C}^{ESQ}=18\text{ }\!\!~\!\!\text{ }X\text{ }\!\!~\!\!\text{ }2=36\text{}\!\!~\!\!\text{ }kN \\ M\text{ }\!\!~\!\!\text{ }m\text{ }\!\!\acute{\mathrm{a}}\!\!\text{ }x=\frac{q{{l}^{2}}}{8}+26=\frac{12\text{ }\!\!~\!\!\text{ }x\text{ }\!\!~\!\!\text{ }{{3}^{2}}}{8}+36=13,5+36\text{ }\!\!~\!\!\text{ }kN \\ M\text{ }\!\!~\!\!\text{ }m\text{ }\!\!\acute{\mathrm{a}}\!\!\text{ }x=49,5\text{ }\!\!~\!\!\text{ }kN\]

Os pórticos são elementos estruturais compostos de vigas e colunas conectadas por ligações rígidas. O ângulo entre a viga e a coluna normalmente é de 90°.
Os pórticos podem ser divididos em duas categorias: contraventados e não contraventados. Pórtico contraventado é aquele no qual os nós em cada nível estão livres para girar, mas são impedidos de se mover lateralmente pela fixação em um elemento rígido que pode fornecer-lhes restrição lateral. Por exemplo, em um prédio de vários andares, os pórticos estruturais são frequentemente ligados aos pilares-paredes (paredes estruturais rígidas, em geral construídas de concreto armado ou
alvenaria armada) (c). Em pórticos simples de um vão, pode ser utilizado um contraventamento diagonal leve, conectado à base das colunas, para resistir ao deslocamento lateral dos nós superiores (d).
Pórtico não contraventado (e) é aquele no qual a resistência lateral ao deslocamento é fornecida pela rigidez à flexão das vigas e colunas. Nos pórticos não contraventados, os nós estão livres para deslocar lateralmente, assim como para girar. Como tendem a ser relativamente flexíveis comparados aos pórticos contraventados, sob carga lateral os pórticos não contraventados podem sofrer grandes deflexões transversais que danificam os elementos não estruturais associados, como paredes, janelas etc.
(LEET; UANG; GILBERT, 2010, pag. 170)

Embora as vigas e as colunas de pórticos rígidos transmitam força axial, força cortante e momento, a força axial nas vigas normalmente é tão pequena que pode ser desprezada, e a viga, dimensionada somente para momento. Faremos apenas uma análise de primeira ordem; isto é, não consideraremos o cálculo do momento secundário — um assunto normalmente abordado em cursos avançados de mecânica estrutural. Como desprezamos os momentos secundários, a análise dos pórticos é semelhante à análise das vigas; isto é, a análise está concluída quando estabelecemos os diagramas de cortante e de momento (além da força axial) com base na geometria inicial do pórtico descarregado.
(LEET; UANG; GILBERT, 2010, pag. 171)
Pórticos são estruturas lineares constituídas por barras retas ligadas entre si. Eles podem ser planos (bidimensionais) ou espaciais (tridimensionais). Trabalharemos apenas com pórticos planos.
Nos pórticos, as ligações entre as barras são engastes ou rótulas internas. Isso faz com que sua estrutura trabalhe em conjuntos e não de forma individual como acontece em estruturas de colunas e vigas. Os Diagramas de Esforço Normal (DEN) e Diagramas de Esforço Cortante (DEC) devem ser traçados para se obter os valores máximos de cada esforço interno para fins de dimensionamento.
No pórtico mostrado como exemplo abaixo, mostramos com linhas tracejadas a forma defletida produzida por uma única carga concentrada, aplicada em meio vão na viga mestra BD de um pórtico contraventado. Em um pórtico contraventado, todos os nós são impedidos de se deslocar lateralmente pelos apoios ou pelas barras conectadas aos apoios imóveis. Para plotar a forma defletida, mostramos a coluna saindo do engaste em A na direção vertical.
A curvatura produzida pelo momento indica que a seção menor da coluna desenvolve tensões compressivas sobre a face externa e tração na face interna. No ponto onde o momento se reduz a zero — o ponto de inflexão (PI) —, a curvatura inverte e a coluna se curva novamente em direção ao nó B. A carga aplicada curva a viga mestra para baixo, fazendo o nó B girar no sentido horário e o nó D no sentido anti-horário. Como o nó B é rígido, o ângulo entre a coluna e a viga mestra permanece em 90°.
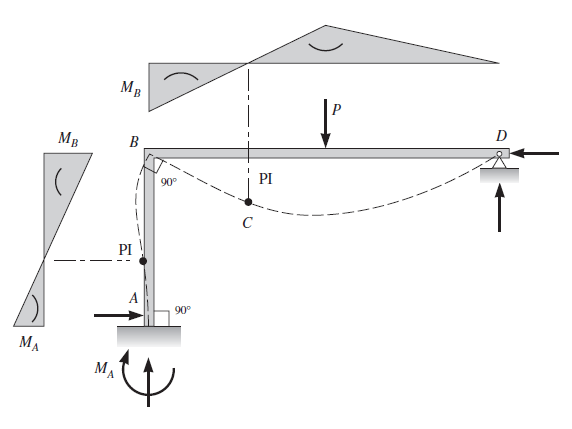
Considerando os sinais dos diagramas, podemos considerar que as fibras inferiores serão tracejadas, definindo, portanto, a parte à esquerda e à direita da seção.

Observe o exemplo abaixo, traçaremos os diagramas de momentos fletores e esforços cortantes dessas estruturas. A imagem ao lado mostra a seção traçada para obter os momentos causados nas barras.

Cálculo das reações:
\[ {{F}_{x}}=0~\to ~{{R}_{AX}}=1~tf \\ {{F}_{y}}=0~\to ~{{R}_{Ay}}=3+1~x~4+1\to ~{{R}_{Ay}}=8~tf~ \\ {{M}_{A}}=0~\to ~3~x~2-1~x~4~x~2-1~x~1+{{M}_{A}}~\to ~{{M}_{A}}=1~tf\]
N = 0;
V = -3 tf
MC = -6 tf.m
N = 0;
V = 1.x
Para x = 0; V = 0;
x = 4; V = 4 tf;
M = -1.x2/2
Para x = 0; M = 0;
x = 4; M = -8 tf.m;
N = -1 tf
V = 1 tf
M = -1.x
Para x = 0; M = 0;
x = 1; M = -1 tf.m;
N = -7 tf
V = 0
M = -2 tf.m
N = -8 tf
V = -1 tf

Aula Concluída!
Avançar